Dentro do mesmo princípio adotado no post Passe de Mágica, em que muitas pessoas conhecem o fato, e o assumem como verdadeiro com uma naturalidade surpreendente, mas não o porquê do fato, dissertarei sobre conceitos e principais propriedades da potenciação visando demonstrar que a0 = 1, para a diferente de zero, muito embora não tenha significado como operação, em vista da definição de potenciação dada abaixo. Como se verá trata-se, como no caso do post mencionado acima, de uma demonstração muito simples (ou trivial no linguajar matemático).

I. DEFINIÇÕES

Vamos começar do começo – eita que frase arretada! – definindo, de maneira simples e direta, que potenciação de um número relativo a nada mais é do que a multiplicação reiterada de a por ele mesmo um número n de vezes, n inteiro e positivo. Ou seja:

Definição de Potenciação

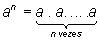
onde se estabeleceu a notação (ou representação simbólica) an para indicar de forma resumida e simplificada (e, diga-se, criativa) esse produto, denominando-se a a base da potência e n o expoente ou grau da potência. Se lê a representação simbólica an como “potência n de a” ou “potência enésima de a” ou “a elevado a n“.

Potência de grau n de a é o produto de n fatores iguais a a. Assim:

  • a0 é a potência de grau zero de a ou potência de expoente zero, a um número real diferente de zero;
  • a1 é a potência de grau 1 de a, sendo igual ao próprio a. Neste caso é dispensável escrever o expoente;
  • a2 é a potência de grau 2 de a, conhecida como quadrado de a ou a ao quadrado;
  • a3 é a potência de grau 3 de a, conhecida como o cubo de a ou a ao cubo.

II. PROPRIEDADES DA POTENCIAÇÃO

a) A potência de grau n de um produto é igual ao produto das potências de grau n dos fatores deste produto. Ou seja:

[1] (abc)n = an.bn.cn [2]

A recíproca também é verdadeira.

Antes de apresentar a demonstração vale explicitar o que significa recíproca. Tomando a igualdade acima, a justificação da propriedade deve ser feita partindo-se de [1] para obter [2]. A recíproca (como o próprio nome diz) é feita partindo-se de [2] para obter [1].

Demonstração:[1] -> [2]

Por definição:

Demonstração da Propriedade a)

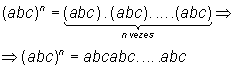
Como a ordem dos fatores de um produto não altera o produto, temos:

Demonstração da Propriedade a)

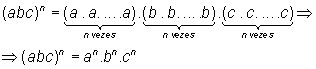
Reciprocamente ([2] -> [1]):

Demonstração da Propriedade a)

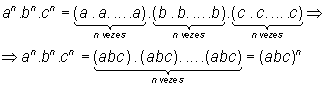
b) O produto de potências de uma mesma base é igual à potência desta base, cujo expoente é a soma dos expoentes dos fatores:

am.an = am+n

Em outras palavras, em um produto de potências com a mesma base, conserva-se a base e soma-se os expoentes. A recíproca é verdadeira.

Demonstração:

Demonstração da Propriedade b)

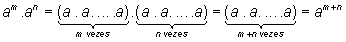
A recíproca deixo por conta do leitor.

c) O quociente de potências de um mesma base é igual à potência desta base, cujo expoente é a diferença entre os expoentes do dividendo e do divisor; isto é:

am/an = am-n, a diferente de zero

Em outras palavras, em um quociente de potências com a mesma base, conserva-se a base e subtrai-se os expoentes. A recíproca é verdadeira.

Demonstração:

Suponhamos que m > n. Então:

Demonstração da Propriedade c)

Eliminando o fator comum ao dividendo e divisor [(a.a … a) n vezes], obtemos:

Demonstração da Propriedade c)

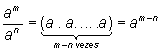
A demonstração da recíproca é fácil, como o de resto, e fica para o leitor se exercitar.

d) A potência n da potência m de um número relativo a é igual a potência de a cujo expoente é o produto dos expoentes m e n, ou seja:

(am)n = amn

A recíproca é verdadeira.

Se você chegou até aqui, obrigado pelo interesse. Em vez da demonstração aproveito para colocar algumas considerações:Matemática se aprende com o entendimento dos seus conceitos, de saber interpretar as questões, dos porquês da verdade de cada assertiva (as demonstrações) e, principalmente, muita transpiração. Por isso pratique e pratique, pois sómente assim você desenvolve melhor sua capacidade de raciocínio para solucionar problemas e fixar os conceitos.

É com este espírito que deixo como exercício a demonstração desta propriedade. Caso tenha dificuldades entre em contato ou deixe seu comentário. Estarei por aqui pronto para atendê-lo.

e) Potência de expoente negativo de um número relativo a diferente de 0:

a-m = 1/am

A recíproca é verdadeira.

Demonstração:

Antes de demonstrar esta propriedade, farei a demonstração do fato que originou este artigo, i.é, a0 = 1, a diferente de zero. Vamos lá.

Por um lado temos que am/am = 1. E por outro, pela propriedade c) que am/am = am-m = a0 => a0 = 1. Trivial, não.

Agora, fica mais fácil demonstar a propriedade. Primeiro:

a-m = a0-m

Pela propriedade c:

a-m = a0/am = 1/am c.q.d. (como queríamos demonstrar).

A recíproca, mais uma vez deixo como exercício.

E, finalmente, sem entrar no mérito, apresento algumas regras de como proceder com o cálculo de potências em que a base é um número negativo.

  • Se o expoente é par, o resultado é positivo;
  • Se o expoente é ímpar, o resultado é negativo.

Faça seus comentários. Apresente sugestões e na medida do possível procurarei lhe atender.

[ATUALIZAÇÃO] 26/03/2006: Veja o artigo publicado sobre radiciação.

[ATUALIZAÇÃO] 24/04/2006: Veja o artigo publicado sobre Equações Exponenciais.

Referência: Abecedário de Álgebra de Darcy Leal de Menezes.

Recomendo fortemente a leitura do artigo Dificuldades para aprender Matemática, publicado no site Tecnociência por Domingos Verena.

Artigos Relacionados:

  1. Questionarious #1 – Potenciação e Radiciação
  2. Produtos Notáveis
  3. Exercícios Resolvidos #1 – Potenciação
  4. Logaritmo
  5. VICHE Responde #1
  6. Equações Exponenciais
  7. Radiciação

Powered by YARPP.