Dentro do mesmo princípio adotado no post Passe de Mágica, em que muitas pessoas conhecem o fato, e o assumem como verdadeiro com uma naturalidade surpreendente, mas não o porquê do fato, dissertarei sobre conceitos e principais propriedades da potenciação visando demonstrar que a0 = 1, para a diferente de zero, muito embora não tenha significado como operação, em vista da definição de potenciação dada abaixo. Como se verá trata-se, como no caso do post mencionado acima, de uma demonstração muito simples (ou trivial no linguajar matemático).
I. DEFINIÇÕES
Vamos começar do começo – eita que frase arretada! – definindo, de maneira simples e direta, que potenciação de um número relativo a nada mais é do que a multiplicação reiterada de a por ele mesmo um número n de vezes, n inteiro e positivo. Ou seja:
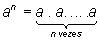
onde se estabeleceu a notação (ou representação simbólica) an para indicar de forma resumida e simplificada (e, diga-se, criativa) esse produto, denominando-se a a base da potência e n o expoente ou grau da potência. Se lê a representação simbólica an como “potência n de a” ou “potência enésima de a” ou “a elevado a n“.
Potência de grau n de a é o produto de n fatores iguais a a. Assim:
- a0 é a potência de grau zero de a ou potência de expoente zero, a um número real diferente de zero;
- a1 é a potência de grau 1 de a, sendo igual ao próprio a. Neste caso é dispensável escrever o expoente;
- a2 é a potência de grau 2 de a, conhecida como quadrado de a ou a ao quadrado;
- a3 é a potência de grau 3 de a, conhecida como o cubo de a ou a ao cubo.
II. PROPRIEDADES DA POTENCIAÇÃO
a) A potência de grau n de um produto é igual ao produto das potências de grau n dos fatores deste produto. Ou seja:
[1] (abc)n = an.bn.cn [2]
A recíproca também é verdadeira.
Antes de apresentar a demonstração vale explicitar o que significa recíproca. Tomando a igualdade acima, a justificação da propriedade deve ser feita partindo-se de [1] para obter [2]. A recíproca (como o próprio nome diz) é feita partindo-se de [2] para obter [1].
Demonstração:[1] -> [2]
Por definição:
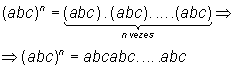
Como a ordem dos fatores de um produto não altera o produto, temos:
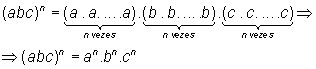
Reciprocamente ([2] -> [1]):
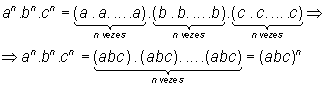
b) O produto de potências de uma mesma base é igual à potência desta base, cujo expoente é a soma dos expoentes dos fatores:
am.an = am+n
Em outras palavras, em um produto de potências com a mesma base, conserva-se a base e soma-se os expoentes. A recíproca é verdadeira.
Demonstração:
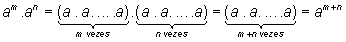
A recíproca deixo por conta do leitor.
c) O quociente de potências de um mesma base é igual à potência desta base, cujo expoente é a diferença entre os expoentes do dividendo e do divisor; isto é:
Em outras palavras, em um quociente de potências com a mesma base, conserva-se a base e subtrai-se os expoentes. A recíproca é verdadeira.
Demonstração:
Suponhamos que m > n. Então:

Eliminando o fator comum ao dividendo e divisor [(a.a … a) n vezes], obtemos:
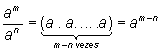
A demonstração da recíproca é fácil, como o de resto, e fica para o leitor se exercitar.
d) A potência n da potência m de um número relativo a é igual a potência de a cujo expoente é o produto dos expoentes m e n, ou seja:
A recíproca é verdadeira.
Se você chegou até aqui, obrigado pelo interesse. Em vez da demonstração aproveito para colocar algumas considerações:Matemática se aprende com o entendimento dos seus conceitos, de saber interpretar as questões, dos porquês da verdade de cada assertiva (as demonstrações) e, principalmente, muita transpiração. Por isso pratique e pratique, pois sómente assim você desenvolve melhor sua capacidade de raciocínio para solucionar problemas e fixar os conceitos.
É com este espírito que deixo como exercício a demonstração desta propriedade. Caso tenha dificuldades entre em contato ou deixe seu comentário. Estarei por aqui pronto para atendê-lo.
e) Potência de expoente negativo de um número relativo a diferente de 0:
A recíproca é verdadeira.
Demonstração:
Antes de demonstrar esta propriedade, farei a demonstração do fato que originou este artigo, i.é, a0 = 1, a diferente de zero. Vamos lá.
Por um lado temos que am/am = 1. E por outro, pela propriedade c) que am/am = am-m = a0 => a0 = 1. Trivial, não.
Agora, fica mais fácil demonstar a propriedade. Primeiro:
a-m = a0-m
Pela propriedade c:
a-m = a0/am = 1/am c.q.d. (como queríamos demonstrar).
A recíproca, mais uma vez deixo como exercício.
E, finalmente, sem entrar no mérito, apresento algumas regras de como proceder com o cálculo de potências em que a base é um número negativo.
- Se o expoente é par, o resultado é positivo;
- Se o expoente é ímpar, o resultado é negativo.
Faça seus comentários. Apresente sugestões e na medida do possível procurarei lhe atender.
[ATUALIZAÇÃO] 26/03/2006: Veja o artigo publicado sobre radiciação. [ATUALIZAÇÃO] 24/04/2006: Veja o artigo publicado sobre Equações Exponenciais.Referência: Abecedário de Álgebra de Darcy Leal de Menezes.
Recomendo fortemente a leitura do artigo Dificuldades para aprender Matemática, publicado no site Tecnociência por Domingos Verena.






jan 26, 2007 @ 08:35:49
Tenho uma equação que não consigo saber o passo a passo para resolver. Ela é simples, porem não consegui chegar aos valores que o livro informa que eu deveria chegar. A equação é:
lim (1 + r / j)^j = e^r
j –> infinito
Não sou matemático, sou biólogo e preciso da resposta para compreender um estudo demográfico. Como o que escrevi na equação está meio estranho vou lê-la: (1 mais r dividido por j) elevado a j é igual a logaritmo nigeriano elevado a r. O valor de r é 0,032 ou 3,2 (não sei bem qual usar) e o esperado é: se j = 2 então o r do nigeriano é 3,1748, se j = 4 então o r do nigeriano é igual a 3,1623 e se j = 12 então o r do nigeriano é 3,1540. Desculpe a falta de conhecimento matemático, não é min ha praia.
Mais uma pergunta, que livros indica que eu compre para saber bem como lidar com equações ou expressões contendo logaritmo, exponencial, e também, matriz. Vou estudar sozinho.
Se puder ajudar resolverá um grande problema para mim. Muito obrigado
jan 03, 2007 @ 14:36:09
Amei este site, pois sou apaixonada por matemática. Porém tenho uma grande dúvida relacionada a potência de mesma base: Sei que em multiplicação conserva-se a base e somam-se os expoentes e em divisão conserva-se a base e subtrai-se os expoentes e em adição de potência de mesma base, o que pode fazer?
dez 17, 2006 @ 11:47:53
OIIIIIIIIII
QUERIA SABER COM SE RESOLVE UMA CONTA QUANDO TEM QUE USAR AS PROPRIEDADES DAS POTÊNCIAS DE MESMA BASE,REDUZINDO A SÓ UMA PÓTÊNCIA DE CADA UMA DAS EXPRESSÕES
7 ELEVADO A 10 . 7 ELEVADOA 12
E (-6) ELEVADO A 3 . (-6)ELEVADO A 15
MUITO OBRIGADO PELA SUA ATENÇAO
BJJJJJJJJJ PRA VCS QUE LER ESSA MENSAGEM
dez 08, 2006 @ 13:14:28
Olá, pesso que me ajude na seguinte expressão (ela é da UFRJ):
(1/ *1 + *2) + (1/ *2 + *3) + (1/ *3 + *4) … (1/*99 + *100)
Coloquei o símbolo * para representar a raíz (quadrada em ambos os termos)
Por favor me ajude… abraços e aguardo resposta
dez 02, 2006 @ 11:03:06
Tenho problema com meu irmão em relação a matematica pesso total ajuda!!!
out 24, 2006 @ 15:09:37
gostaria de saber como faço para elevar um numero racional tipo 1/2 sobre outro numero racional 2/4?
se existe, pos ´pesquisei e so achei intero elevado a racional, se puder me ajudar. Obrigado.
out 18, 2006 @ 12:14:17
Bom, tenho uma certa dificuldade com potenciação,
e gostaria de entender como posso calcular manualmente potencias elevadas à expoentes grandes como..
2 elevado a 999
não faço ideia por onde começar..
poderiam me ajudar ???
out 05, 2006 @ 20:53:23
ficou boa, mais não entendi muito bem como calcular e ACHAR o expoente inteiro negativo…tenho um trabalho sobre isso e nós estamos um tanto enrolados porque nunca vimos essa matéria, e estamos no primeiro ano, daí complica…
set 23, 2006 @ 15:04:33
Na verdadede tenho duas duvidas .
gostaria de saber a propriedadeque define potenciação de polinomios por ex: qual seria o resultado de (x+h) elevado à -2 e (x+h) elevado a 1/2
muito grato
set 21, 2006 @ 19:03:24
estou conhecendo o site agora,e espero aprender muito, e tirar as minhas dúvidas,principalmente em expreções algébricas.
—!@!—
set 11, 2006 @ 01:53:21
Não consigo resolver este problema: COMO SABEMOS QUE 3 NÃO DIVIDE NENHUMA POTÊNCIA DE 10?
set 08, 2006 @ 09:35:05
Qual o resto da divisão:
2941elevado a 317 divido por 11.
Gostaria de saber passo a passo.
ago 31, 2006 @ 15:45:53
a^0=1 porque??? se a^2=a.a=a^2; a^1=a.1=a; a^0=1a.0=0.
ago 31, 2006 @ 10:47:09
pah adorei esse saite pois agente aprende muito !!
eu queria saber mais sobre logaritimos !!!
ago 29, 2006 @ 08:54:54
se eu tiver uma equação de (x+y) ao cubo como a resolvo, responda para o e-mail ok, obrigado
ago 24, 2006 @ 17:25:24
Preciso resolver este problema podes me ajudar?
(1/2am+y²)-(1/3am+2y²)-1/6am=
ago 24, 2006 @ 17:22:12
tenho uma filha na 7ª série com muitos problemas, preciso forma simples para demonstrar e explicar este cálculo. podes me ajudar?
(1/2am+y²)-(1/3am+2y²)-1/6am=
Grata
ago 21, 2006 @ 01:01:07
gostaria de saber por gentileza se,numeros negativos elevado ao expoente zero é igual a um positivo ?
ago 14, 2006 @ 23:07:17
QUERO SABER MAIS SOBRE MATÉMATICA EM ELETRÔNICA.
ago 14, 2006 @ 11:09:26
olá tenho uma questão para resolver e eu gostaria de saber como faço para resolve-la (1+i )¹²-1 / i (1+i)¹²
ago 12, 2006 @ 10:31:15
ESSE SITE É MUITO BOM E FÁCIL DE SE ENTENDER . VALEU PELA AJUDA!!!
ago 08, 2006 @ 14:08:12
oi gostaria de saber pq todo numero elevado a zero vale um?
ago 04, 2006 @ 12:52:57
oi, tenho um trabalho para fazer sobre Potenciação, Estou no 1º ano do ensino médio. Um item que deve ser pesquisado é NOME DOS TERMOS da potenciação. Queria saber o que é.
Obrigada.
ago 02, 2006 @ 16:24:23
Fernanda,
Sua questão está desvinculada do assunto abordado. Mas, como se trata de um desafio interessante vai ai a solução:
5!/(5 + 5 + 5) = 120/15 = 8
onde, para quem não sabe, 5! = 5 x 4 x 3 x 2 x 1 = 120, e significa fatorial de 5 ou 5 fatorial.
ago 02, 2006 @ 14:09:18
disculpa o nome la eh fernanda
ago 02, 2006 @ 14:08:14
estou com um problema e não consigo resolver eh um desafio
usando 4 numeros 5 para obter como resultado 8 podendo usar qual quer operação matemática
ex:
55-55=0
55/55=1
5/5+5/5=2
5+5+5=15/5=3
gostaria muito da ajuda de alguem se porerem ajudar fikarei muito grata
jul 25, 2006 @ 10:18:23
Estou com dificuldades para resolver 5/3 elevado a 2028… Se puderem ajudar-me ficarei muito agradecido. Abraços
jul 19, 2006 @ 15:43:05
Olá,
Hoje acessei pela primeira vez este site.Tenho filhos no ensino fundamental e preciso ajudá-los em época de provas, devo confessar que foi sensacional, pois aqui consigo, após décadas sem rever tais assuntos, relembrar facilmente todas as matérias.
Abraços
jul 18, 2006 @ 00:11:57
newton,
embora ainda não tenha conseguido visualizar a sua resposta (problema no servidor) agradeço desde já pela sua atenção.
até breve
jul 13, 2006 @ 10:09:12
Cátia,
Veja esta explicação.
jul 13, 2006 @ 00:24:13
parabéns, gostei muito do site, e gostaria de saber como é possível resolver esse tipo de exercício:
determinar o resto da divisão por 5 do produto 83942^359 X 7859^267 X 948^179 X 7496^323.
e ou a onde posso obter maiores informações para resolver esse tipo de atividade,´pois estou procurando e não acho em lugar algum.
obrigada.
jul 02, 2006 @ 19:43:51
Parabéns,gostaria de saber qual é a resolução prática da radiciação:raiz quadrada de 856 e/ou raiz cúbica de 1745.
muito obrigado.Ass-Homero Soares
jun 28, 2006 @ 18:28:48
“”Oi!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
eu preciso de problemas de .5série é com numeros pro hoje porque eu preciso estudar e amanha é prova é eu não vou estar
aqui amanha então eu presciso pra agora(meu caderno eu esqueci na casa da minha vó) porfavor
Obrigada
jun 27, 2006 @ 09:01:11
Felipe,
231.526 = 25226526= 32.1026
Logo o número de algarismos é igual a 28 (32 + 26 zeros).
jun 26, 2006 @ 20:03:22
por favor como respondo essa??
o numero de algarismos do numero natural 2 elevado a 31 vezes 5 elevado 26? ja procurei em varios livros e não encontrei ajuda ai caras!!!!
jun 23, 2006 @ 02:10:15
GOSTARIA DE SABER COMO SURGIU A POTENCIAÇÃO – A HISTORIA DA POTENCIAÇÃO ALGO ASSIM, EU ADORO POTENCIA.
AVALEU.
OBRIGADA.
jun 17, 2006 @ 12:32:55
Afonso,
Soma-se os expoentes quando temos um produto de potências com a mesma base – veja Propriedade b). Exemplo: 25.27 = 25+7 = 212
Subtrai-se os expoentes quando temos o quociente de potências com a mesma base – veja Propriedade c). Exemplo: 35/32 = 35-2 = 33
Se ainda tem dúvidas, dê uma espiada na aplicação destas propriedades no artigo Exercícios Resolvidos 1 – Potenciação.
jun 17, 2006 @ 12:07:12
gostaria q me de-sem esclarecimentos de como e quando temos q somar os expoentes ou subtrai-los isso cria-me transtornos serios
jun 14, 2006 @ 20:45:35
Ariovaldo,
Veja a Propriedade P7 do artigo sobre Radiciação publicado aqui no Blog. Tente resolver e caso não consiga entre em contato.
jun 14, 2006 @ 19:38:14
Gostaria de saber como resolver: (3/4)^4/3 ou (3/4)^3/2. Obrigado.
jun 14, 2006 @ 09:49:22
Paula,
O resultado da operação 5256 é um número muito grande, que corresponde, pela definição de potência, ao produto de 5 por ele mesmo 256 vezes. E, portanto, torna-se impraticável efetuar este cálculo manualmente.
Agora, você pode expressar este resultado, por exemplo, como uma outra potência 8,6361685550944446253863518628004e+178 através de cálculo efetuado em uma calculadora. Veja que, mesmo assim, é ainda um número de difícil interpretação.
Ou você pode expressá-lo como o antilogaritmo de 256 na base 5 (não sei se você conhece) ou outra expressão, mas o valor exato só para os computadores!
jun 13, 2006 @ 20:21:42
OI, gostei muito so site….
Tenho uma certa dificuldade com potenciação, e gostaria de saber a resposta do item 12
como posso resolver : 5 elevado a 256 ?
jun 10, 2006 @ 17:53:12
Por favro, preciso resolver urgente a equação (1/2) elevado a n = 0,03125. Não consigo saber qual a propriedade que me leva ao valor de n. Que relação há para achar o valor de n????
Viche » Exercícios Resolvidos #1 - Potenciação
jun 07, 2006 @ 00:53:57
[…] Nas soluções dos exercícios serão mencionadas as propriedades pela letra utilizada no artigo sobre potenciação . […]
jun 05, 2006 @ 18:18:46
Faço faculdade de matemática aqui na bahia econheci esse site agora. Eu n tive muito tempo para olhar com mais atenção esse site, mas tudo que eu li foi muito bom. Cara estou encantado com como você alia rigor e simplicidade de uma forma impressionante. você é bom demais viu!!!!
Fantástico!
um abraço!!!!
jun 04, 2006 @ 21:45:27
Esse site é excelente!!!!
jun 04, 2006 @ 20:54:45
gostaria de saber quantos litros equivale a 1m³
maio 30, 2006 @ 08:52:53
por que que todo número diferente de zero elevado ao expoente zero é igual a um?
maio 29, 2006 @ 23:43:01
Beatriz,
(1 + i)12 = (1 + i) … (1 + i) [doze vezes] pela definição de potenciação. E portanto, não é igual a 112 + i12. Veja que não se aplica para a soma a propriedade equivalente válida para o produto (a.b)n = an.bn.
maio 29, 2006 @ 23:27:50
Eu gostaria de saber se está correto o seguinte exercício:
(1 + i) elevado hà potencia 12 é igual a 1 elevado hà 12 + i elevado a 12 ?