Vamos abordar neste post as propriedades referentes à redução de frações. Alguns conceitos aqui utilizados encontram-se no post Frações – Parte I que podem – e devem – ser consultados em caso de dúvidas.
Redução de Frações
Reduzir uma fração é transformá-la em uma outra equivalente.
Tá legal. Mas o que são frações equivalentes? São aquelas que mantêm a mesma proporção de outra fração, ou seja, é a fração obtida, de uma outra, multiplicando-se ou dividindo-se o seu numerador e o denominador por um mesmo número diferente de zero (veja propriedade 6 da primeira parte).
Exemplo: 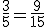 . Veja que a segunda fração é obtida a partir da primeira multiplicando-se o seu numerador e seu denominador por 3. Inversamente, a primeira é obtida da segunda dividindo-se o seu numerador e seu denominador, também, por 3.
. Veja que a segunda fração é obtida a partir da primeira multiplicando-se o seu numerador e seu denominador por 3. Inversamente, a primeira é obtida da segunda dividindo-se o seu numerador e seu denominador, também, por 3.
Os principais procedimentos de redução de frações são:
- Reduzir inteiros a frações impróprias;
- Reduzir números mistos a frações impróprias;
- Extrair inteiros de frações impróprias;
- Simplificar frações;
- Reduzir frações ao mesmo denominador.
Leia Mais ...
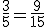 . Veja que a segunda fração é obtida a partir da primeira multiplicando-se o seu numerador e seu denominador por 3. Inversamente, a primeira é obtida da segunda dividindo-se o seu numerador e seu denominador, também, por 3.
. Veja que a segunda fração é obtida a partir da primeira multiplicando-se o seu numerador e seu denominador por 3. Inversamente, a primeira é obtida da segunda dividindo-se o seu numerador e seu denominador, também, por 3.




Comentários Recentes