INTRODUÇÃO

No artigo publicado em 23 de fevereiro de 2006, aqui no VICHE, abordei a definição e propriedades da potenciação. Caso você não tenha o domínio desse assunto, sugiro a sua leitura, visando uma melhor compreensão do que será exposto a seguir. O interesse demonstrado pelo tema foi e ainda permanece considerável, tomando-se por base o número de visitas ao artigo (1030 até o momento em que escrevia este post, segundo dado estatístico fornecido pelo software Webalizer). Agora, dando continuidade, trataremos da radiciação de números relativos e expressões algébricas.

Serão tratados os conceitos e propriedades da radiciação sob o ponto de vista primordialmente teórico, como no da potenciação, acrescidos de alguns exemplos. No entanto, caso seja demonstrado interesse, estarei criando uma seção específica (aceito sugestões para o seu nome) com o objetivo de responder, com o devido detalhamento, a questões e dúvidas colocadas nos comentários ou enviadas para o E-Mail nghorta@brturbo.com.br. As soluções serão fornecidas dentro do mesmo padrão aqui adotado, uma vez que é praticamente inviável de serem apresentadas diretamente no formulário dos comentários, devido às restrições ali impostas.

Apenas uma ressalva: por limitação de tempo, pois tenho que ganhar o pão nosso de cada dia, do trabalho que dar escrever artigos de matemática (estou “matutando” escrever um post sobre este fato) e em função da demanda, talvez não tenha condições de responder a todas as dúvidas e questões. Porém, prometo fazer todo o esforço necessário para não deixar nenhuma de fora. Por último, solicito que as questões sejam elaboradas da forma mais clara possível e se reportem, preferencialmente, ao assunto que está sendo tratado – no caso radiciação.

DEFINIÇÃO

Radiciação de números relativos é a operação inversa da potenciação. Ou seja,

Em outros termos, dado um número relativo a denominado radicando e dado um número inteiro positivo n denominado índice da raiz, é possível determinar outro número relativo b, denominado raiz enésima de a (ou raiz de índice n de a), representada pelo símbolo , tal que b elevado a n seja igual a a.

Antes de partir para o próximo tópico – as propriedades da radiciação – algumas observações importantes e exemplos:

• O símbolo <=> indicado na fórmula acima significa se e sómente se. Isto é, se a expressão antes desse símbolo é verdadeira então a segunda também é, e vice-versa;.
• Na definição acima, temos que bⁿ = a. Substituindo o valor de b (segunda igualdade), obtemos que , i.e., a potência de grau n da raiz enésima de a é igual a a;
• é o símbolo de raiz ou sinal de raiz ou simplesmente radical;
• Radical, além de ser o símbolo acima indicado, é também, por extensão, a raiz de um número relativo ou de uma expressão algébrica;
• Raiz de índice 1 (n = 1) de a é o próprio número a;
• Raiz de índice 2 (n = 2) de a é denominada de raiz quadrada de a. Neste caso não é necessário escrever o índice n no radical;
• Raiz de índice 3 (n = 3) de a é denominada de raiz cúbica de a;
• Extração da raiz enésima de a é o cálculo dessa raiz;
• O valor da raiz enésima de a nem sempre é um número racional (inteiro ou fracionário), uma vez que nem sempre a é uma potência de grau n, n inteiro, de b (por exemplo: raiz quadrada de 2);
• Mesmo nesses casos é possível representar a raiz como uma potência de expoente fracionário (detalhes serão fornecidos mais a frente), embora sem significado como operação (exemplo: a raiz quadrada de 2 é expressa como 2^1/2);
• Erro de aproximação, é o erro cometido na extração da raiz enésima de a, em que não existe uma potência de grau n, n inteiro, de b que seja igual a a (por exemplo: raiz quadrada de 2 cujos valores aproximados podem ser 1; 1,4; 1,41; 1,414; …);
• Raízes de índice par pode não ter solução válida no conjunto dos números reais (por exemplo: a raiz quadrada de -1, uma vez que a potência de grau par de um número é sempre positiva);
• Para dar consistência ao cálculo de raízes de índice par e radicando com valor negativo, foi criado o conjunto dos números complexos, com a introdução da unidade imaginária i, cujo valor corresponde à raiz quadrada de -1;
• Valor aritmético ou valor absoluto de um radical é o valor positivo desse radical (exemplo: o valor aritmético da raiz quadrada de 4 é +2, embora -2 também satisfaça a definição);
• No cálculo dos radicais, conjunto de operações com números irracionais e com expressões algébricas, são considerados sempre apenas o seu valor aritmético, ou seja, seu valor positivo. Os valores positivos e negativos, quando é o caso, são adotados principalmente na resolução de equações polinomiais, como por exemplo, em uma equação do segundo grau;
• Radicais equivalentes são os que têm o mesmo valor aritmético (exemplo: raiz cúbica de 8 e raiz quadrada de 4 são equivalentes por que ambas têm valor aritmético igual a 2);
• Radicais semelhantes são os que têm o mesmo índice e o mesmo radicando. Veja exemplo abaixo.

Exemplos:

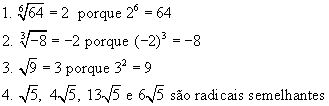
PROPRIEDADES

Apenas algumas das propriedades abaixo serão demonstradas, deixando a verificação das demais como exercício. Havendo manifestação de interesse poderei publicar um post específico com a verificação das propriedades não apresentadas.

P1. A raiz enésima do produto a.b é igual ao produto das raízes enésimas de a e b:

Demonstração:

Da definição de radiciação, temos que:

Por outro lado, utilizando-se a propriedade da potência de grau n de um produto, e, novamente, a definição de radiciação, obtemos:

Como se vê dos passos anteriores, foi demonstrado que ambos os lados da igualdade da propriedade elevado ao expoente n é igual ao produto a.b. Portanto, a base dessas potências são necessariamente iguais e a verificação da propriedade está concluída.

Aplicação prática da Propriedade (simplificação de radicais):

P2. O produto das raízes de a e de b com o mesmo índice n é igual a raiz enésima do produto a.b (note que esta propriedade é a recíproca de P1. Nas demais propriedades a recíproca também é válida. Esclarecimentos do que se entende por recíproca você pode obter no artigo sobre Potenciação ):

A demonstração de P2 é semelhante à de P1.

P3. O quociente de raízes de mesmo índice n é igual a raiz enésima do quociente dos radicandos:

P4. A potência de grau m da raiz de índice n de a é igual a raíz de índice n de a elevado à potência m:

Demonstração:

Para demonstrar a propriedade P4 utilizarei a técnica de demonstração por indução sobre m, considerando n fixo, que consiste em:

1. A propriedade é verdadeira para m = 0, pois

2. Considerando que P4 é verdadeira para m = p, m > 0, isto é:

provemos que é verdadeira para m = p + 1, ou seja:

De fato:

Observe que na expressão acima utilizamos a hipótese (verdadeira para m = p), a propriedade P2 e a propriedade de produtos de potências de mesma base.

3. Considerando agora m < 0 façamos -m = q > 0, então:

Na expressão acima foram utilizadas a propriedade de potência de expoente negativo, a hipótese, a propriedade P3 e regra de divisão de frações.

P5. A raiz de índice m de uma raiz de índice n de a é igual à raiz de índice mn de a:

P6. A raiz enésima de a elevado a m é igual a raiz de índice p.n de a elevado a p.m obtida multiplicando-se o índice e radicando por p. A mesma propriedade é válida para a divisão:

Exemplo: Redução de radicais ao mesmo índice

P7. A raiz de índice n da potência de grau m de a é igual à potência de grau m/n de a:

Demonstração:

Da propriedade P6, dividindo-se o índice e o radicando por n:

Exemplos:

É interessante observar que todas as propriedades de potências para expoentes inteiros positivos são válidas, também, para as potências de expoentes fracionários.

Referências:

1. Abecedário da Álgebra (Volume 1 – Ciclo Ginasial), Darcy Leal de Menezes, Rio de Janeiro, Departamento de Imprensa Nacional, primeira edição, 1959;
2. Fundamentos de Matemática Elementar, Gelson Iezzi, Osvaldo Dolce & Carlos Murakami, São Paulo, Atual Editora Ltda, edição 1977.

Posts Relacionados

1. Questionarious #1 – Potenciação e Radiciação
2. Curiosidade Matemática #5 – Método de Pitágoras para Calcular a Potência de Grau 2 de um Número
3. Exercícios Resolvidos #3 – Radiciação
4. Exercícios Resolvidos #1 – Potenciação
5. Logaritmo
6. VICHE Responde #1
7. Potenciação

Posts relacionados trazidos a você pelo Yet Another Related Posts Plugin.