INTRODUÇÃO
No artigo publicado em 23 de fevereiro de 2006, aqui no VICHE, abordei a definição e propriedades da potenciação. Caso você não tenha o domínio desse assunto, sugiro a sua leitura, visando uma melhor compreensão do que será exposto a seguir. O interesse demonstrado pelo tema foi e ainda permanece considerável, tomando-se por base o número de visitas ao artigo (1030 até o momento em que escrevia este post, segundo dado estatístico fornecido pelo software Webalizer). Agora, dando continuidade, trataremos da radiciação de números relativos e expressões algébricas.
Serão tratados os conceitos e propriedades da radiciação sob o ponto de vista primordialmente teórico, como no da potenciação, acrescidos de alguns exemplos. No entanto, caso seja demonstrado interesse, estarei criando uma seção específica (aceito sugestões para o seu nome) com o objetivo de responder, com o devido detalhamento, a questões e dúvidas colocadas nos comentários ou enviadas para o E-Mail nghorta@brturbo.com.br. As soluções serão fornecidas dentro do mesmo padrão aqui adotado, uma vez que é praticamente inviável de serem apresentadas diretamente no formulário dos comentários, devido às restrições ali impostas.
Apenas uma ressalva: por limitação de tempo, pois tenho que ganhar o pão nosso de cada dia, do trabalho que dar escrever artigos de matemática (estou “matutando” escrever um post sobre este fato) e em função da demanda, talvez não tenha condições de responder a todas as dúvidas e questões. Porém, prometo fazer todo o esforço necessário para não deixar nenhuma de fora. Por último, solicito que as questões sejam elaboradas da forma mais clara possível e se reportem, preferencialmente, ao assunto que está sendo tratado – no caso radiciação.
DEFINIÇÃO
Radiciação de números relativos é a operação inversa da potenciação. Ou seja,

Em outros termos, dado um número relativo a denominado radicando e dado um número inteiro positivo n denominado índice da raiz, é possível determinar outro número relativo b, denominado raiz enésima de a (ou raiz de índice n de a), representada pelo símbolo  , tal que b elevado a n seja igual a a.
, tal que b elevado a n seja igual a a.
Antes de partir para o próximo tópico – as propriedades da radiciação – algumas observações importantes e exemplos:
- O símbolo <=> indicado na fórmula acima significa se e sómente se. Isto é, se a expressão antes desse símbolo é verdadeira então a segunda também é, e vice-versa;.
- Na definição acima, temos que bn = a. Substituindo o valor de b (segunda igualdade), obtemos que
, i.e., a potência de grau n da raiz enésima de a é igual a a;
 é o símbolo de raiz ou sinal de raiz ou simplesmente radical;
é o símbolo de raiz ou sinal de raiz ou simplesmente radical;- Radical, além de ser o símbolo acima indicado, é também, por extensão, a raiz de um número relativo ou de uma expressão algébrica;
- Raiz de índice 1 (n = 1) de a é o próprio número a;
- Raiz de índice 2 (n = 2) de a é denominada de raiz quadrada de a. Neste caso não é necessário escrever o índice n no radical;
- Raiz de índice 3 (n = 3) de a é denominada de raiz cúbica de a;
- Extração da raiz enésima de a é o cálculo dessa raiz;
- O valor da raiz enésima de a nem sempre é um número racional (inteiro ou fracionário), uma vez que nem sempre a é uma potência de grau n, n inteiro, de b (por exemplo: raiz quadrada de 2);
- Mesmo nesses casos é possível representar a raiz como uma potência de expoente fracionário (detalhes serão fornecidos mais a frente), embora sem significado como operação (exemplo: a raiz quadrada de 2 é expressa como 21/2);
- Erro de aproximação, é o erro cometido na extração da raiz enésima de a, em que não existe uma potência de grau n, n inteiro, de b que seja igual a a (por exemplo: raiz quadrada de 2 cujos valores aproximados podem ser 1; 1,4; 1,41; 1,414; …);
- Raízes de índice par pode não ter solução válida no conjunto dos números reais (por exemplo: a raiz quadrada de -1, uma vez que a potência de grau par de um número é sempre positiva);
- Para dar consistência ao cálculo de raízes de índice par e radicando com valor negativo, foi criado o conjunto dos números complexos, com a introdução da unidade imaginária i, cujo valor corresponde à raiz quadrada de -1;
- Valor aritmético ou valor absoluto de um radical é o valor positivo desse radical (exemplo: o valor aritmético da raiz quadrada de 4 é +2, embora -2 também satisfaça a definição);
- No cálculo dos radicais, conjunto de operações com números irracionais e com expressões algébricas, são considerados sempre apenas o seu valor aritmético, ou seja, seu valor positivo. Os valores positivos e negativos, quando é o caso, são adotados principalmente na resolução de equações polinomiais, como por exemplo, em uma equação do segundo grau;
- Radicais equivalentes são os que têm o mesmo valor aritmético (exemplo: raiz cúbica de 8 e raiz quadrada de 4 são equivalentes por que ambas têm valor aritmético igual a 2);
- Radicais semelhantes são os que têm o mesmo índice e o mesmo radicando. Veja exemplo abaixo.
Exemplos:
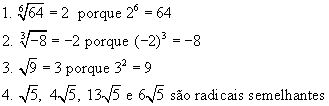
PROPRIEDADES
Apenas algumas das propriedades abaixo serão demonstradas, deixando a verificação das demais como exercício. Havendo manifestação de interesse poderei publicar um post específico com a verificação das propriedades não apresentadas.
P1. A raiz enésima do produto a.b é igual ao produto das raízes enésimas de a e b:

Demonstração:
Da definição de radiciação, temos que:
Por outro lado, utilizando-se a propriedade da potência de grau n de um produto, e, novamente, a definição de radiciação, obtemos:
Como se vê dos passos anteriores, foi demonstrado que ambos os lados da igualdade da propriedade elevado ao expoente n é igual ao produto a.b. Portanto, a base dessas potências são necessariamente iguais e a verificação da propriedade está concluída.
Aplicação prática da Propriedade (simplificação de radicais):
P2. O produto das raízes de a e de b com o mesmo índice n é igual a raiz enésima do produto a.b (note que esta propriedade é a recíproca de P1. Nas demais propriedades a recíproca também é válida. Esclarecimentos do que se entende por recíproca você pode obter no artigo sobre Potenciação ):

A demonstração de P2 é semelhante à de P1.
P3. O quociente de raízes de mesmo índice n é igual a raiz enésima do quociente dos radicandos:
P4. A potência de grau m da raiz de índice n de a é igual a raíz de índice n de a elevado à potência m:

Demonstração:
Para demonstrar a propriedade P4 utilizarei a técnica de demonstração por indução sobre m, considerando n fixo, que consiste em:
1. A propriedade é verdadeira para m = 0, pois
2. Considerando que P4 é verdadeira para m = p, m > 0, isto é:
provemos que é verdadeira para m = p + 1, ou seja:
De fato:
Observe que na expressão acima utilizamos a hipótese (verdadeira para m = p), a propriedade P2 e a propriedade de produtos de potências de mesma base.
3. Considerando agora m < 0 façamos -m = q > 0, então:
Na expressão acima foram utilizadas a propriedade de potência de expoente negativo, a hipótese, a propriedade P3 e regra de divisão de frações.
P5. A raiz de índice m de uma raiz de índice n de a é igual à raiz de índice mn de a:

P6. A raiz enésima de a elevado a m é igual a raiz de índice p.n de a elevado a p.m obtida multiplicando-se o índice e radicando por p. A mesma propriedade é válida para a divisão:

Exemplo: Redução de radicais ao mesmo índice
P7. A raiz de índice n da potência de grau m de a é igual à potência de grau m/n de a:

Demonstração:
Da propriedade P6, dividindo-se o índice e o radicando por n:
Exemplos:
É interessante observar que todas as propriedades de potências para expoentes inteiros positivos são válidas, também, para as potências de expoentes fracionários.
Referências:
- Abecedário da Álgebra (Volume 1 – Ciclo Ginasial), Darcy Leal de Menezes, Rio de Janeiro, Departamento de Imprensa Nacional, primeira edição, 1959;
- Fundamentos de Matemática Elementar, Gelson Iezzi, Osvaldo Dolce & Carlos Murakami, São Paulo, Atual Editora Ltda, edição 1977.





jun 10, 2009 @ 23:03:35
Olá, tudo bem? gostei bastante do artigo, tudo está muito bem explicado, mas minha dúvida não está nele, por isso acho que poderia perguntar. Eu estava estudando equaçõs do segundo grau e polinômios e estou com umas dificuldades de chegar a certos resultados… minha dúvida é sobre a diferença conceitual entre a²=x e a=raiz de x, com relação aos sinais.
Abraços
jun 04, 2009 @ 14:01:19
Pow,eu tenho prova hoje de matematica,como ta encima da hora ,eu estudei no caderno,e vim aki na net pra confirmar se eu aprendi mesm.obrigado pq eu ja aprendi vlw
jun 02, 2009 @ 20:34:35
Olha eu tenho uma duvida, como isso pode se aplicar no nosso cotidiano, ja procurei em um monte de site e nao achei nada. Me ajua?
maio 24, 2009 @ 14:06:44
estou cursando matematica,e gostaria de uma orintação de como fazer para escrever as regras e as definições de potenciação para que os alunos de sexta serie possam ler e entender de forma mais simples e mais rapidas
maio 09, 2009 @ 14:26:55
eu amo matematica!!mas ñ consiguo entender
maio 08, 2009 @ 17:14:01
Gostaria de agradecer por esta site de informacoes , principalmente na cadeira de matematica . contudo sugeria que adicionacem mas exercicios e debates.
Atentamente
Salomao Mendes
abr 27, 2009 @ 11:13:45
a Paula a Yarlla e eu Camila barros amomos esse site…..
bjusssssssss3333333
888888 77777
+++++++
abr 23, 2009 @ 16:22:23
gostaria de saber como resolver RAIZ QUADRADA DE ( X elevado a 2 ) – 6x + 9
abr 20, 2009 @ 23:00:53
eu acho esse assunto muito interesante…
abr 12, 2009 @ 15:52:05
Não consegui entender como calcular a raiz enesima de um numero qualquer. Os exemplos me parecem direcionados a facilitar a explicação, no entanto não fica claro como aplica-los. Por exemplo, como devemos proceder para calcular a raiz quinta de 342, cujo equivalente em potenciação será 342^1/5?
abr 11, 2009 @ 16:52:09
ola pessoal, estou com dificuldade em chegar no resultado do seguinte exercicio.
raiz quadrada de nove menos entre parenteses raiz de cinco elevado a sexta com expoente a um terço mais entre parenteses raiz quadrada de sete elevado ao expoente meio.
e ai como chego no resultado.
desde ja agradeço pela ajuda.
abr 05, 2009 @ 20:06:36
Gostaria de mais conhecimento sobre simplificação de radicais ,
retirando fatores do radicando ! Desde já agradeço . ! ;)
abr 05, 2009 @ 17:09:58
eu odeio matematica
abr 03, 2009 @ 10:00:55
como calcula a raiz de 1/2????
mar 24, 2009 @ 17:03:55
gostaria de ver exercicios de simplificações de radicais porque estou com difilculdades para entnder
mar 23, 2009 @ 01:51:43
O que é uma raiz enésima?
mar 15, 2009 @ 15:29:24
gostei da materia e muito lagal p apredremos mais sobre fatoracoes e a raizes etc………
mar 04, 2009 @ 10:14:15
Ola..eu tenho alguns problemas com fatoraçoes algebricas. Quem puder me ajudar..eu agradeço!! =D
fev 04, 2009 @ 16:29:26
foi muito interessante passar por aq e saber muito mais
jan 13, 2009 @ 22:23:34
Estou com a seguinte dúvida: raíz quarta de 2 multiplicada pela raíz quadrada de seis é igual a dois elevado a três quartos multiplicado por três elevado a um meio?
Acho que esta igualdade não esta correta.
Quem puder me ajudar agradeço!
dez 10, 2008 @ 15:12:26
a ajuda foi boa vlw
out 16, 2008 @ 16:51:44
oi,eu entendi muito bem,mas eu estou proucurando uma forma de resolver a seguinte questão: raiz cubica de três elevado a um vírgula cinco.
já tentei de tud e nao consigo resolver.
gostaria q vc me ajudase.
obrigado.
out 14, 2008 @ 12:27:08
por favor, vc poderia passar pra mim exemplos de simplificaçôes ds radicais, tenho muitas dúvidas a repeito.
Obrigado!
out 07, 2008 @ 15:12:31
Gostaria de ter uma ajuda para fazer esse programinha.
Faça um programa que leia um número inteiro X e
um expoente inteiro n.
O programa deve calcular e exibir o resultado,
ou seja X elevado a n.
obs: usar uma estrutura de repetição
Plz! Ty!
set 28, 2008 @ 14:42:17
Por favor gostaria de saber como posso resolver a seguinte questão: Raiz cúbica de 2 elevado a 28 mais 2 elevado a 30 dividido por 10. Se puder me ajudar agradeço muito. Obrigada.
set 06, 2008 @ 13:25:40
oi, Tudo bem?gostei do seu artigo ele explica detelhadamente o básico sobre raiz, mas eu gostaria de saber o seguinte:
como é q prova q a raiz enesima da raiz enesima …… de um numero “a” é igual a 1
set 02, 2008 @ 12:35:07
O trabalho é muito bom. No entanto seria perfeito se houvesse uma seção onde enviássemos dúvidas e elas fossem respondidas para todos. Assim ampliaria exponenciamente o conhecimento dos internautas.
Obrigado
julio
set 01, 2008 @ 15:55:00
voces estao de parabens pelas publicaçoes escelentes sobre as materias de matematica que têm fornecido à gente. gostaria que passacem a passar exercicios ao meu e-mail.
ago 05, 2008 @ 14:18:53
gostaria que voces falassem sobre as propriedades dos numeros reais e radicais pois eu tenho trabalhos de matematica que pede este conteudo e nao tem obrigada pela atencao
atenciosamente :
Karinne de Oliveira Carvalho
jul 05, 2008 @ 22:43:09
Eu acho muito interessante professor nenhum ensinar nas escolas, como se calcular a raíz quadrada sem o uso de
calculadoras. A raíz cúbica então, nem se fala.
Por experiência própria, me lembro perfeitamente, quando
fazendo o curso de MADUREZA na década de 70, pedí ao
professor p/ explicar como calcular a raíz quadrada de um
número. O mesmo “enrolou” até o fim do ano sempre com uma
desculpa, mas nunca explicou nada.
Aprendí com muito custo, depois de vários anos numa
matéria que encontrei na INTERNET e ensinei meu filho,
KLEBER AUGUSTO BARBO a extrair essa raíz, já explicando
que na escola ele jamais iria aprender.
Hoje, ele é mestre na arte da extração da raíz quadrada a
ponto de desconsertar sua professora. Quero apenas dizer
que meu filho tem apenas 11 anos e grande capacidade de
aprendizado.
Por que ninguém fala nada sôbre a raíz cúbica, sem usar
a fórmula de NEWTON, que é desesperadora?
Quero acreditar que a raíz cúbica deva ser parecida com
a raíz quadrada, na fórmula, ou será tão diferente assim?
João Valentim Barbo
jul 05, 2008 @ 07:00:40
DIRETO, COERENTE E SIMPLES.
Muito bom material, você me fez lembrar de um antigo professor de matemática, foi este professor que me abriu o entendimento e me fez gostar de matemática.
Já pensou em escrever um livro didático para matemática, talvez você já o tenha feito e eu é que não o conheça! Deixei o banco das escolas há mais de 50 anos.
uma das principais causas do péssmo grau de aproveitamento no ensino brasileiro na área de matemática é que a maioria dos livros didáticos de matemática são escritos para quem já conhece matemática, daí vem o desastre! Os autores de livros de matemática fundamental utilizam a linguagem matemática para explicar matemática, como fazem isto logo no princípio do aprendizado de matemática a maioria dos alunos tomam ojeriza pela área e adeus bons alunos de matemática, se você se propor a publicar o livro para o ensino de matemática! Pode utilizar o pomposo título: DANDO NOME AOS BOIS, (matemática simplificada), vai ser um sucesso…
A propósito, a palavra é devagarzinho.
Edimilson
jun 23, 2008 @ 20:42:52
Nossa adorei o site,eu estava com duvida,acabei lendo e entendendo!!!obrigada
maio 15, 2008 @ 11:59:03
peeelo amor de deus.. me ajudou demais essa explicação.. primeira vez que visito esse site.. ta de parabens cara! =D
abraços pra todos.
maio 08, 2008 @ 16:59:35
qual o resultado de:
raiz cúbica de a/b e dentro dela raiz quadrada de a/b?
maio 08, 2008 @ 14:35:42
muito bom
maio 03, 2008 @ 16:12:01
Amigos,
Tenho a seguinte questão a resolver: a=raiz décima segunda (12) de 1,84. São dadas as seguintes informações:
a) Raiz cúbica de 1,84=1,22538514.
b) Raiz quarta de 1,84=1,1646742.
c) Raiz sexta de 1,84= 1,10697115.
Com base nestas informações qual propriedade da radiciação eu poderia utilizar para a resolução da questão?
Agradeço se puderem me ajudar.
Noel Barreto.
maio 02, 2008 @ 17:09:56
vc poderia me repassar um exemplo de simplificaçôes ds radicais
por favor me repasse URGENTE
eu estou precisando
abr 24, 2008 @ 19:26:41
ahhh foi bom ter pesquisado ai pqeu inha que fazer um adependencias e nao tava a chando nada e soh entcontrei aqui vcs precisa ter tbm sobre radicalização de denominadores sobre matématica
abr 16, 2008 @ 21:04:27
Muito bom …
Me ajudou bastante a relembrar alguns fatores sobre radiciação q tinha esquecido …
MUitoo bom ..
Abraços e beijos ..
abr 09, 2008 @ 21:00:41
obrigada quem quer que seja.
abr 09, 2008 @ 12:12:30
achei muito podre esse site!!!!!!!!!!
q site de 5 categoria………shahsahshasahshsah..
abr 07, 2008 @ 15:51:25
está muito bom!
mas se explicasse com mais clareza iria ser mais fácil de entender!!
abr 03, 2008 @ 22:43:07
eu não achei oque eu estava procurando
abr 03, 2008 @ 13:21:09
qual e a raiz quadrada de 32?
abr 03, 2008 @ 12:05:29
como eu resolvo essa aii ó> raiz sexta ,o radical (a) com o expoente (7) x (z) com o expoente (13) ?
abr 02, 2008 @ 16:11:38
Eu nao consigo entender o que é radiciaçao
mar 31, 2008 @ 21:14:04
Oi,,sou um estudante da 8ª série q,incrivelmente,adora matemática.Gostaria de agradecer por esse site,que tirou uma dúvida mto grande de dentro de mim sobre Radiciação,MTO OBRIGADO!!!!
mar 23, 2008 @ 19:51:24
oi professor. obg essa explicação me ajudou muito, salvou minha pele. bjão.
mar 16, 2008 @ 18:00:27
o segundo exemplo esta erra (-2) elevado ao cubo. da -8 e nao 8
mar 15, 2008 @ 18:16:39
odeiooooooooooooooooooooooooooooooo matematica