INTRODUÇÃO
No artigo publicado em 23 de fevereiro de 2006, aqui no VICHE, abordei a definição e propriedades da potenciação. Caso você não tenha o domínio desse assunto, sugiro a sua leitura, visando uma melhor compreensão do que será exposto a seguir. O interesse demonstrado pelo tema foi e ainda permanece considerável, tomando-se por base o número de visitas ao artigo (1030 até o momento em que escrevia este post, segundo dado estatístico fornecido pelo software Webalizer). Agora, dando continuidade, trataremos da radiciação de números relativos e expressões algébricas.
Serão tratados os conceitos e propriedades da radiciação sob o ponto de vista primordialmente teórico, como no da potenciação, acrescidos de alguns exemplos. No entanto, caso seja demonstrado interesse, estarei criando uma seção específica (aceito sugestões para o seu nome) com o objetivo de responder, com o devido detalhamento, a questões e dúvidas colocadas nos comentários ou enviadas para o E-Mail nghorta@brturbo.com.br. As soluções serão fornecidas dentro do mesmo padrão aqui adotado, uma vez que é praticamente inviável de serem apresentadas diretamente no formulário dos comentários, devido às restrições ali impostas.
Apenas uma ressalva: por limitação de tempo, pois tenho que ganhar o pão nosso de cada dia, do trabalho que dar escrever artigos de matemática (estou “matutando” escrever um post sobre este fato) e em função da demanda, talvez não tenha condições de responder a todas as dúvidas e questões. Porém, prometo fazer todo o esforço necessário para não deixar nenhuma de fora. Por último, solicito que as questões sejam elaboradas da forma mais clara possível e se reportem, preferencialmente, ao assunto que está sendo tratado – no caso radiciação.
DEFINIÇÃO
Radiciação de números relativos é a operação inversa da potenciação. Ou seja,

Em outros termos, dado um número relativo a denominado radicando e dado um número inteiro positivo n denominado índice da raiz, é possível determinar outro número relativo b, denominado raiz enésima de a (ou raiz de índice n de a), representada pelo símbolo  , tal que b elevado a n seja igual a a.
, tal que b elevado a n seja igual a a.
Antes de partir para o próximo tópico – as propriedades da radiciação – algumas observações importantes e exemplos:
- O símbolo <=> indicado na fórmula acima significa se e sómente se. Isto é, se a expressão antes desse símbolo é verdadeira então a segunda também é, e vice-versa;.
- Na definição acima, temos que bn = a. Substituindo o valor de b (segunda igualdade), obtemos que
, i.e., a potência de grau n da raiz enésima de a é igual a a;
 é o símbolo de raiz ou sinal de raiz ou simplesmente radical;
é o símbolo de raiz ou sinal de raiz ou simplesmente radical;- Radical, além de ser o símbolo acima indicado, é também, por extensão, a raiz de um número relativo ou de uma expressão algébrica;
- Raiz de índice 1 (n = 1) de a é o próprio número a;
- Raiz de índice 2 (n = 2) de a é denominada de raiz quadrada de a. Neste caso não é necessário escrever o índice n no radical;
- Raiz de índice 3 (n = 3) de a é denominada de raiz cúbica de a;
- Extração da raiz enésima de a é o cálculo dessa raiz;
- O valor da raiz enésima de a nem sempre é um número racional (inteiro ou fracionário), uma vez que nem sempre a é uma potência de grau n, n inteiro, de b (por exemplo: raiz quadrada de 2);
- Mesmo nesses casos é possível representar a raiz como uma potência de expoente fracionário (detalhes serão fornecidos mais a frente), embora sem significado como operação (exemplo: a raiz quadrada de 2 é expressa como 21/2);
- Erro de aproximação, é o erro cometido na extração da raiz enésima de a, em que não existe uma potência de grau n, n inteiro, de b que seja igual a a (por exemplo: raiz quadrada de 2 cujos valores aproximados podem ser 1; 1,4; 1,41; 1,414; …);
- Raízes de índice par pode não ter solução válida no conjunto dos números reais (por exemplo: a raiz quadrada de -1, uma vez que a potência de grau par de um número é sempre positiva);
- Para dar consistência ao cálculo de raízes de índice par e radicando com valor negativo, foi criado o conjunto dos números complexos, com a introdução da unidade imaginária i, cujo valor corresponde à raiz quadrada de -1;
- Valor aritmético ou valor absoluto de um radical é o valor positivo desse radical (exemplo: o valor aritmético da raiz quadrada de 4 é +2, embora -2 também satisfaça a definição);
- No cálculo dos radicais, conjunto de operações com números irracionais e com expressões algébricas, são considerados sempre apenas o seu valor aritmético, ou seja, seu valor positivo. Os valores positivos e negativos, quando é o caso, são adotados principalmente na resolução de equações polinomiais, como por exemplo, em uma equação do segundo grau;
- Radicais equivalentes são os que têm o mesmo valor aritmético (exemplo: raiz cúbica de 8 e raiz quadrada de 4 são equivalentes por que ambas têm valor aritmético igual a 2);
- Radicais semelhantes são os que têm o mesmo índice e o mesmo radicando. Veja exemplo abaixo.
Exemplos:
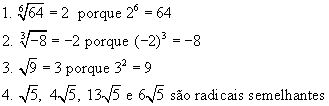
PROPRIEDADES
Apenas algumas das propriedades abaixo serão demonstradas, deixando a verificação das demais como exercício. Havendo manifestação de interesse poderei publicar um post específico com a verificação das propriedades não apresentadas.
P1. A raiz enésima do produto a.b é igual ao produto das raízes enésimas de a e b:

Demonstração:
Da definição de radiciação, temos que:
Por outro lado, utilizando-se a propriedade da potência de grau n de um produto, e, novamente, a definição de radiciação, obtemos:
Como se vê dos passos anteriores, foi demonstrado que ambos os lados da igualdade da propriedade elevado ao expoente n é igual ao produto a.b. Portanto, a base dessas potências são necessariamente iguais e a verificação da propriedade está concluída.
Aplicação prática da Propriedade (simplificação de radicais):
P2. O produto das raízes de a e de b com o mesmo índice n é igual a raiz enésima do produto a.b (note que esta propriedade é a recíproca de P1. Nas demais propriedades a recíproca também é válida. Esclarecimentos do que se entende por recíproca você pode obter no artigo sobre Potenciação ):

A demonstração de P2 é semelhante à de P1.
P3. O quociente de raízes de mesmo índice n é igual a raiz enésima do quociente dos radicandos:
P4. A potência de grau m da raiz de índice n de a é igual a raíz de índice n de a elevado à potência m:

Demonstração:
Para demonstrar a propriedade P4 utilizarei a técnica de demonstração por indução sobre m, considerando n fixo, que consiste em:
1. A propriedade é verdadeira para m = 0, pois
2. Considerando que P4 é verdadeira para m = p, m > 0, isto é:
provemos que é verdadeira para m = p + 1, ou seja:
De fato:
Observe que na expressão acima utilizamos a hipótese (verdadeira para m = p), a propriedade P2 e a propriedade de produtos de potências de mesma base.
3. Considerando agora m < 0 façamos -m = q > 0, então:
Na expressão acima foram utilizadas a propriedade de potência de expoente negativo, a hipótese, a propriedade P3 e regra de divisão de frações.
P5. A raiz de índice m de uma raiz de índice n de a é igual à raiz de índice mn de a:

P6. A raiz enésima de a elevado a m é igual a raiz de índice p.n de a elevado a p.m obtida multiplicando-se o índice e radicando por p. A mesma propriedade é válida para a divisão:

Exemplo: Redução de radicais ao mesmo índice
P7. A raiz de índice n da potência de grau m de a é igual à potência de grau m/n de a:

Demonstração:
Da propriedade P6, dividindo-se o índice e o radicando por n:
Exemplos:
É interessante observar que todas as propriedades de potências para expoentes inteiros positivos são válidas, também, para as potências de expoentes fracionários.
Referências:
- Abecedário da Álgebra (Volume 1 – Ciclo Ginasial), Darcy Leal de Menezes, Rio de Janeiro, Departamento de Imprensa Nacional, primeira edição, 1959;
- Fundamentos de Matemática Elementar, Gelson Iezzi, Osvaldo Dolce & Carlos Murakami, São Paulo, Atual Editora Ltda, edição 1977.




abr 26, 2011 @ 14:36:54
Eu gostei, consegui entender algumas coisas pois minha professora não explicou a matéria e tenho prova, vou agora fazer algumas expressões.. pra ver se consegui mesmo.. Adorei
abr 25, 2011 @ 19:21:54
ESSE SITE E UM DOS MELHORES Q JAH VI ENTODO ESSE TEMPO
abr 18, 2011 @ 16:09:50
muito bom mais so ki os exemplos naum kerem aparecer
abr 16, 2011 @ 15:06:48
eu gostei de site por que ele esplica tudo que vc procurar
abr 25, 2011 @ 17:53:15
explica é com x e não com s ok???
abr 13, 2011 @ 19:20:23
eu to fazendo um trabalho sobre esse assunto e tipo eu vim direto nesse site é muito bacana agente saber sobre esse assunto.beijos thamyres e quem precisar de ajuda eu posso ajudar…
abr 13, 2011 @ 19:14:00
é muito bacana esse site por que é be, explicado e ajuda agente saber mais sobre isso.beijos e obrigada
abr 08, 2011 @ 14:38:40
EEU QUERIIA MUITO SABER QUAL A ORIIGEM DE ONDE SURGIIU A RADICIAÇÃO =( SE ALGUÉM PUDER ME AJUDAR AEEE PLEASE EU QUEROO TUDO MSM , PRA UM TRABALHO =( // BJUUUSTINS’
abr 07, 2011 @ 17:37:36
putz que dificil
caraca e muito show
caralhoooooo
mar 21, 2011 @ 20:19:14
espero tirar 10 em meu trabalho : ]
mar 21, 2011 @ 18:24:53
bom espero tirar uma boa nota em meus trabalhos !!!
rs” *; )
mar 19, 2011 @ 12:45:55
adorei o melhor site que eu encontrei na internet
fev 22, 2011 @ 16:28:26
gostei
fev 19, 2011 @ 15:28:26
Melhor explicação que encontrei na internet ;*
nov 10, 2010 @ 08:11:14
Falta um conteúdo muito importante sobre raízes de raízes. ;P
nov 08, 2010 @ 20:43:54
Gostei meee ajudou muiito
rsrsrsrsrsrsrs blw
ago 06, 2010 @ 17:06:42
LOEGAL………
DEU P/ TIRAR ALGUMAS DUVIDAS QUE EU TINHA…
jun 29, 2010 @ 14:49:38
Bom, tá muito ótima a explicação, más eu quero saber certinho o QUE É RAIZ CÚBICA, e naum como se resolve!
Valew!
Bjinhos
jun 17, 2010 @ 14:59:39
bom deu p entender,só espero num tirar + notas baixas esse site me ajudou muito a fazer a pesquisa.=D
jun 16, 2010 @ 05:38:36
√4 = (+2)
√4 = (- 2)
Então: (+2) = ( -2) …????
jun 10, 2010 @ 19:30:11
o site é bom, mas precisa de algo melhor explicado,
algumas coisas estao confusas….
Vlw
:)
maio 31, 2010 @ 10:28:24
estou na mira da cascavel
maio 18, 2010 @ 16:50:55
ñ~gostei nao ta explicando nada e nem tem exemplo
maio 12, 2010 @ 14:24:31
nunca pensei que encotraria matéria explicada de uma forma tão simples, tão simples e, mesmo a distáncia deu pra perceber tudinho valeu brother.
Ulianov da Silva- Luanda Angola
maio 06, 2010 @ 00:35:53
Muito boa matéria. Quem inventou não interessa. Mas que eu tô ficando boa nisso aí… Ah isso só as provas vão me dizer…
Obrigada para vc que criou este site!
Merece um beijãaaaaaaaaaaaaaaaaaaaaaaaaaaao…
maio 05, 2010 @ 16:59:45
Oiie Gente (y)
Olha pessoal acho que ficou faltando assunto
Tipo, Quem inventou / Quando Surgiu etc..
maio 01, 2010 @ 14:54:39
achei esta explicação a melhor de todas que encontrei na net, parabens.
abr 29, 2010 @ 15:04:55
bom , eu não enteendii muiitoo beem naa escoolaa , maais depois quee eu li essa explicação melhorou muiito ‘
Valeeeeu (y)
abr 16, 2010 @ 11:57:02
legal me ajudou muito.Mas será que vocês poderiam me enviar algumas questões que envolvam esse assunto ? De já agradeço.
abr 06, 2010 @ 20:28:00
não ajudo em nada¬¬
abr 06, 2010 @ 12:47:45
muito bacana essas esplicacoes…..xau
mar 25, 2010 @ 15:04:49
a radiciação é o inverso da potenciação..
vcs diviam aprender isso na escola
vem fazer o trabalho com a gente pra ve como vcs vão aprender alguma coisa que o professor Paquito ensina.E a gente aprende viiu
ele eh um otimo professor pois a gente aprende muito com ele so naum sabe como fazer os exercícios e a introdução q a gente veio buscar aqui mais naum encontramos nada de bom
por favor alguem da proxima vez coloca algo q preste e q a gente consiga entender tah
obrigada xau
mar 20, 2010 @ 17:46:44
Mas quem fez essa teoria, tão incrível?
mar 18, 2010 @ 01:36:46
Ok. Mas na expressão “a” elevado a potência “n” =b, como calacular o valor de n?
ex.: 2n=32 (2 elevado a n é igual a 32). qual o vaor de n? como calcular?
mar 17, 2010 @ 16:44:45
na minha opinião esse site eé importante sim maiix ñ contém tudo o que um estudante precisa para aprender “RADICAIS EQUIVALENTES”! que era o que eu vim procurar!
mar 15, 2010 @ 12:26:34
Não entendi nada, acho qe esse negócio ai não é tão esclarecedor, já tem 30 minutos qe eu estou tentando entender alguma coisa disso e NADA. =D
mar 11, 2010 @ 12:33:47
eu adoroooo fazer enesima!!!
mar 04, 2010 @ 16:07:56
uhu facim e nao so nerd tiro nota baixa flw galera(isso nao me ajudou em nada¬¬)
mar 03, 2010 @ 14:26:54
Gostei doo siite :)) bem esclareido !
mar 01, 2010 @ 15:07:11
na minha opinião esse site é importante para os e estudantes…..
tem assuntos na sala de aula que são difíceis
bjjjjjjssss!!!!!!!!
lululuzita
………………………………………………./;./;..~;.;./;./;.;.?:
fev 27, 2010 @ 09:31:01
gostei so que queria tirar mais uma duvida, como calcular raiz quadrada de 2 x raiz quadrada de 2x raiz quadrada de 2
fev 22, 2010 @ 20:41:55
Gostei.. deu pra fazer o relatório rs
Valeu (:
fev 20, 2010 @ 18:21:20
vc acha esse site legal?
nov 30, 2009 @ 21:13:18
deu pra intender…….valeu
gostei
-tirou algumas dúvidas dos assuntos da recuperação de matematica-
nov 29, 2009 @ 12:06:10
to totalmente perdida :@
set 30, 2009 @ 16:54:27
Legal mais msmo assim ñ sei fazer issso…
…Huashuasuahsuahsa…mias um dia eu aprendo..
…Vlw
set 14, 2009 @ 15:22:27
Too perdidoona taambeiim (!)
ago 30, 2009 @ 11:04:36
muito bom sua fomula de explicação!
jul 05, 2009 @ 19:46:00
po tem prova de matematica amanham
valeu deu p tira muitos duvidas
jun 30, 2009 @ 20:58:19
massaa!!**
jun 20, 2009 @ 21:55:58
hmmmmmmmmm……………………..to perdidaaa