Logaritmo foi o assunto escolhido, com 13 votos, na pesquisa realizada pelo VICHE. Para ver o resultado e os detalhes basta clicar no link Consultar Pesquisas localizado na barra lateral de navegação.
Antes de prosseguir com a abordagem do tema vencedor registro os nossos agradecimentos a todos os leitores participantes.
No artigo sobre equações exponenciais citamos os dois principais métodos utilizados para resolver este tipo de equação:
- o de redução a potências de mesma base, e
- o que utiliza o conceito e propriedades de logaritmos.
O primeiro foi tratado naquele artigo com a colocação de conceitos, exemplos e exercícios resolvidos, em que estes, foram propositalmente selecionados, visando apresentar o uso de técnicas diferenciadas na resolução de equações exponenciais.
O segundo será abordado agora, como já dito, com o intuito de auxiliá-lo a resolver equações do tipo 3x = 7, entre outras, em que não é possível reduzir seus termos a uma potência de mesma base.
Apesar de podermos afirmar com facilidade que x assume um valor entre 1 e 2, pois 3 < 3x = 7 < 9, não sabemos qual é exatamente esse valor e nem o processo para determiná-lo, tomando-se por base os conceitos publicados até aqui no VICHE.
Para isto é necessário acrescentar a seu repertório de conhecimentos a definição e propriedades dos logaritmos.
Definição
Dados a e b números reais e positivos, com a diferente de 1, definimos logaritmo de b na base a, o número x, cuja potência de grau x de a é igual a b. Ou seja:
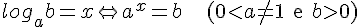
Observações e consequências da definição:
- Na expressão a esquerda a é denominado a base do logaritmo, b o logaritmando e x o logaritmo;
- Como a e b são ambos positivos e a é diferente de 1, existe um único valor de x que satisfaz a primeira igualdade na expressão acima;
- Decorre da definição de logaritmo que loga1 = 0, pois a0 = 1. Em outras palavras, que o logaritmo de 1 em qualquer base é igual 0;
- Do mesmo modo, observe que logaa = 1, uma vez que a potência de grau 1 de a é o próprio a. Ou seja, que o logarítmo da base, qualquer que seja a base satisfazendo, claro, as condições da definição, é igual a 1;
- Substituindo o valor de x da primeira igualdade na segunda, obtemos que alogab = b;
- logab = logac <=> b = c. Decorrência direta da definição (b = alogac) e do fato acima (alogac = c). Traduzindo: dois logaritmos em um mesma base são iguais se e somente se os logaritmandos são iguais;
- Note que de 6. pode-se afirmar, ainda, que em uma igualdade ao se aplicar o logaritmo aos seus membros essa igualdade não se altera;
- Ao conjunto de todos os logaritmos dos números reais positivos em uma base a (a > 0 e diferente de 1), denominamos de sistema de logaritmos de base a;
- Entre a infinidade de sistemas de logaritmos de base a, dois são particularmente importantes: o sistema de logaritmo decimais ou de base 10 e o sistema de logaritmo neperiano (também chamado de sistema de logaritmos naturais) ou de base e (e = 2,71828…, irracional);
- O logaritmo decimal é representado pela notação log10x ou simplesmente log x. E o neperiano por logex ou ln x;
- Fato histórico 1: Henry Briggs, Matemático Inglês (1561-1630) foi quem primeiro destacou a vantagem dos logaritmos de base 10, publicando a primeira tabela (ou tábua) de logaritmos de 1 a 1000 em 1617;
- Fato histórico 2: O nome neperiano vem de John Neper, Matemático Escocês (1550-1617), autor do primeiro trabalho publicado sobre a teoria dos logaritmos. O nome natural é devido ao fato de que no estudo dos fenômenos naturais geralmente aparece uma lei exponencial de base e.
Exemplos:
Antilogaritmo
Sejam a e b dois números reais positivos com a diferente de 1. Se o logaritmo de b na base a é igual a x, então b é o antilogaritmo de x na base a. Em símbolos:
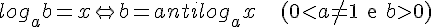
Exemplos:
Propriedades dos Logaritmos
L1. O logaritmo do produto de dois fatores reais e positivos em qualquer base a (a > 0 e diferente de 1) é igual a soma dos logaritmos dos fatores. Isto é:
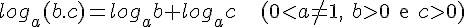
Demonstração:
Fazendo z = loga(b.c) temos, usando a definição de logaritmo, que:
az = b.c
Daqui, obtemos pela observação 5. acima:
az = alogab.alogac => az = alogab+logac => z = logab + logac
Substituindo z na última igualdade fica concluída a demonstração.
Uma outra forma, também simples e similar a anterior, de demonstrar a propriedade L1 é esboçada a seguir. Fazendo:
z = loga(b.c), x = logab e y = logac
vamos provar que z = x + y.
Aplicando a definição de logaritmo nas expressões acima obtemos, respectivamente:
az = bc, ax = b e ay = c
Substituindo b e c na primeira igualdade vem que:
az = axay => az = ax+y => z = x + y
A propriedade L1 é válida para o logaritmo do produto de n fatores (n > 2) reais e positivos, ou seja:
loga(b1.b2. … .bn) = logab1 + logab2 + … + logabn
A prova pode ser feita utilizando-se o método de indução sobre n, que consiste em:
- demonstrar que é verdadeira para n = 2 – já feita;
- supor que é válida para n = p > 2 e demonstrar que é verdadeira para n = p + 1.
Deixo para vocês a demonstração com a seguinte dica: agrupar como produto de dois fatores de modo a aplicar L1 e após utilizar a hipótese para n = p.
L2. O logaritmo do quociente de dois números reais e positivos em qualquer base a (a > 0 e diferente de 1) é igual ao logaritmo do dividendo menos o logaritmo do divisor nessa mesma base. Em símbolos:
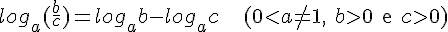
Demonstração:
De maneira semelhante à adotada na propriedade L1, fazendo z = loga(b/c) obtemos:
Como consequência direta da propriedade L2 temos que:
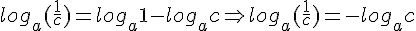
Cologaritmo
Dados a e b dois números reais positivos, com a diferente de 1, define-se cologaritmo de b na base a ao oposto do logaritmo de b nessa base a. Ou seja:
cologab = -logab = loga(1/b)
L3. O logaritmo da potência de grau x de b em qualquer base a (a, b reais positivos, x real e a diferente de 1) é igual ao produto do expoente x pelo logaritmo de b na base a. Em símbolos:
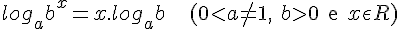
Demonstração:
Novamente fazemos uso do procedimento utilizado na demonstração das propriedades anteriores:
Fica como exercício a demonstração das propriedades L2 e L3 com o uso da segunda técnica adotada para provar a propriedade L1.
Como consequência da propriedade L3 temos que: o logaritmo da raiz de índice n de b na base a é igual ao produto do inverso do índice n pelo logaritmo do radicando na base a, i.e.:
![\Large log_a\sqrt[n]{b}=log_ab^{\frac{1}{n}}=\frac{1}{n}log_ab\hspace{20}(0\lt a\ne1\text{, }b\gt0\text{ e }n\epsilon N^*) \Large log_a\sqrt[n]{b}=log_ab^{\frac{1}{n}}=\frac{1}{n}log_ab\hspace{20}(0\lt a\ne1\text{, }b\gt0\text{ e }n\epsilon N^*)](http://www.blogviche.com.br/mimetex/pictures/bc4aab939c6ffc1a2d27eb3add4b3a10.gif)
Observações sobre as Propriedades L1, L2 e L3
- São válidas somente quando temos expressões logarítmicas que envolvam as operações de multiplicação, divisão e potenciação;
- Essas propriedades não permitem obter o logaritmo de uma soma ou diferença [loga(b + c) ou loga(b – c)]. Nestes casos, será necessário primeiro obter o valor da soma ou da diferença.
Mudança de Base
É muito comum, e você já deve ter se deparado com o fato, ter expressões ou equações logarítmicas em que seus membros estejam em bases diferentes.
Como na aplicação das propriedades operatórias, os logaritmos devem estar todos em uma mesma base é fundamental saber como isto é feito.
Você deve se lembrar (se não, volte às observações) que no início deste artigo mencionei como importante o sistema de logaritmo decimais ou de base 10, para o qual foi construída, pelo matemático Henry Briggs, uma tábua de logaritmos que possibilita determinar o seu valor para qualquer número real positivo.
Não abordaremos aqui os conceitos de mantissa e característica do logaritmo decimal utilizados para determinar seu valor com o auxílio da tabela. Fica apenas o registro de sua importância no uso das propriedades de mudança de base que apresentamos a seguir.
L4. Dados a, b e c números reais positivos, com a e c diferentes de 1, tem-se que:
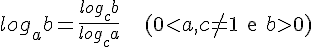
Demonstração:
Fazendo logab = x, logcb = y e logca = z provemos que x = y/z (note que z é diferente de zero, pois por definição a é diferente de 1). De fato:
Como consequência da propriedade L4 temos:
- logab = logcb.logac: a demonstração é feita transformando logcb para a base a no segundo membro da igualdade;
- logab = 1/logba: transforme logab para a base b.
Exercícios Resolvidos
1. Resolver a equação 3x = 7 (lembra-se, a do início do artigo):
Aplicando o logaritmo na base 10 aos dois membros da equação temos:
log 3x = log 7
Pela propriedade L3:
x.log 3 = log 7 => x = log 7/log 3 = 0,845/0,477 = 1,771
2. Um capital de R$50.000,00 foi aplicado a uma taxa de juros compostos de 5% ao ano, e o capital de R$45.000,00 a 6% ao ano. Em quanto tempo os montantes estarão iguais?
Um uso muito comum das propriedades de logaritmo para resolver equações exponencias é no cálculo de juros compostos cuja fórmula é:

onde M é o montante, C o capital, i a taxa de juros e t o tempo.
Solução:
Sejam M1 e M2 os montantes correspondentes aos capitais aplicados. Usando a fórmula, temos que:
M1 = 50000(1 + 0,05)t e M2 = 45000(1 + 0,06)t
Temos que determinar o tempo para que M1 = M2. Assim:
Referência:
- Fundamentos de Matemática Elementar, Gelson Iezzi, Osvaldo Dolce & Carlos Murakami, São Paulo, Atual Editora Ltda, edição 1977.
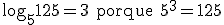
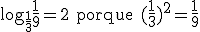
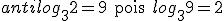
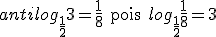






out 10, 2007 @ 12:14:19
estou com duvida nesta questão: log (x-3)=4
2
como posso responder?
out 07, 2007 @ 23:29:43
que bosta esse site, tudo mais complicado ainda.
deleta isso, faça esse bem a humanidade!
desculpe se sou sincera demais, mas eu tinha que dizer..
odiei ;)
out 05, 2007 @ 13:11:17
A cada dia está melhor.Parabéns!!
out 05, 2007 @ 07:20:11
calcular:
logx – log9=1 mas a base do 1º é 3 e do 2º é x
out 01, 2007 @ 21:05:36
Sou formanda de licenciatura em matemática e meu trabalho de conclusão é sobre a aplicação dos logarítmos, atualmente. Será que alguém poderia ajudar-me?
out 01, 2007 @ 10:29:27
oi, eu estudo num supletivo e queria saber sobre log 1000
set 26, 2007 @ 17:14:06
A resolução de vcs caiu na minha prova de matematica hj, porem naum consegui lembrar dela e errei a questao. é vero!!
set 24, 2007 @ 20:40:46
gente pelo amor de deus vou ter uma prova amanhan de matematica e gostaria de saber como eu resolvo(a conta interira) a)log 15
b)log com um tres embaixo de base, e logaritimando: (ab²/c)
c)log com base ³√7 e e logaritimando 49
d)qual é o valor de y=log com base ³√4 e logaritimando √2 +log com base: ³√100 e logaritimando: *√0,1 – log 100?
(*=6)
ficarei mto grata se vcs me ajudarem
set 24, 2007 @ 18:05:43
Ótimo!!!!
conteúdo muito bem organizado e de fácil entendimento!
continue sempre assim!!
abraços
set 23, 2007 @ 01:13:29
como faço pra resolver um numero (x) elevado a um logaritmo!
Ex:(vou escrever por extenso):X elevado a log de (x-1) na base 3 ?
Obrigada.
ago 31, 2007 @ 11:15:17
Eu queria ter uma tabela de todas propridades LOGARITMICAS,
não sei podem ajudar-me nessa situação neste sentido.
Um abraço, escrevo de ANGOLA…..
ago 22, 2007 @ 17:54:32
log x = log 1,035¹² => log x = 12 log 1,035 => log x = 0,1788 => x = 1,509
Favor queria saber detalhadamento como chegar ao resultado x=1,509, pois estou tentando de varias maneiras e não consigo…tbm ja revirei a web inteira e nao consegui!!!
fev 15, 2016 @ 17:35:03
também não consigo.
jul 11, 2007 @ 10:46:37
Acho que tem que ter mais conteudo.Ñ achei exatamente o que esperava encontrar nese site!
jun 25, 2007 @ 22:58:15
Logaritmo é fascinante, mas é complicado!!! O que temos que fazer com o Log é estudar, estudar e estudar…valeu!!!
jun 23, 2007 @ 20:44:08
Eu gostaria de saber quais sao as aplicações dos logaritmos e já revirei toda a web e ainda não encontrei quase nada gostaria de pedir a ajuda do Viche.Então pedido feito,espero alguma resposta.
Bjs.
Babi.
jun 08, 2007 @ 13:35:59
eu qro a tabela d logaritmos..
jun 03, 2007 @ 10:52:44
http://www.dna2007.org/console/console2007.asp
qro v qm resolve…
jun 02, 2007 @ 16:24:33
Nossa achei bem legal o site …. tirei bastante duvidas …
parabens ..
maio 28, 2007 @ 16:43:54
[red]gostaria de saber a resposta deste exercício:
O álcool do sangue de um motorista alcançou o nível de 2g/l ,logo depois de ter bebido uma considerável quantidade de cachaça.considere que seu nível descreve de acordo com a fórmula
t
N(t)=2 x (0,5) ,onde t é o tempo medido em horasa partir do momento em que o nível foi constatado.Quanto tempo deverá o motorista esperar antes de dirigir seu veículo, se o limite permitido de alcool no sangue para dirigir com segurança é de 0,8g/l ?
se possível resolver, agradeço.
maio 25, 2007 @ 11:04:43
Estou com dúvida para resolver as expressões abaixo utilizando o conceito de logaritmo:
7000(1+0,005)N=7500
1000x(1+0,05)N=2500
Obs: Achar o valor de “n” na potência.
Favor enviar modelo de cálculo
maio 24, 2007 @ 20:58:54
Adorei a reportagem.Parabéns aos pesquisadores e ao redator.
maio 09, 2007 @ 14:33:02
Exemplo:
Calcule o montante de um capital de R$6.000,00, aplicado a juros compostos, durante 1 ano, à taxa de 3,5% ao mês.
(use log 1,035=0,0149 e log 1,509=0,1788)
Resolução:
P = R$6.000,00
t = 1 ano = 12 meses
i = 3,5 % a.m. = 0,035
M = ?
Usando a fórmula M=P.(1+i)n, obtemos:
M = 6000.(1+0,035)12 = 6000. (1,035)12
Fazendo x = 1,03512 e aplicando logaritmos, encontramos:
log x = log 1,035¹² => log x = 12 log 1,035 => log x = 0,1788 => x = 1,509
Então M = 6000.1,509 = 9054.
Portanto o montante é R$9.054,00
ENTÃO, (1,035)¹² ONDE O RESULTADO?
OBRIGADO!
maio 09, 2007 @ 14:11:42
muliplicação de bases iguais e expoentes diferentes
abr 24, 2007 @ 19:48:54
– O valor da soma
S= log10 0.001 + log2 (4 raiz quadrada de 32) – log5 0.125
-Determine a solução:
2log2 (x+1) – log2 (x² – 1)
abr 05, 2007 @ 08:02:47
Gostaria que me fosse tirada uma dúvida de matemática:
Qual destas equações está correcta?
120x ao quadrado = 0
x ao quadrado = 0 a dividir por 120
OU
120x ao quadrado = 0
x ao quadrado = 120
abr 03, 2007 @ 15:31:03
isso é chato pra burro
que coisa
mar 25, 2007 @ 15:52:13
Primeiramente mo satisfação em ter um site para tirar duvidas,vocêis estão de parabens,eu sou deficiente fisico e não é sempre que estou em codições de ir a escola as vezes estou doente em fim.Eu gostaria de apreender sobre logaritmando e base e logaritmo estou em dificuldade para apreender tem como vcs me ajudar ficarei agradecido,obrigado vcs estão de parabéns valeu
mar 23, 2007 @ 20:10:29
Como resolvo este exercício?
O IDH – Indice de Desenvolvimento Humano – é um número entre 0 e 1m calculado pela média aritmética de três índices: de educação, de expectativa de vida ao nascer e do PIB em dólares. Com base nesses dados e na comparação entre os países, é possível analisar a qualidade de vida e o desenvolvimento humano no planeta. O cálculo do índice do PIB é feito através da seguinte fórmula:
Índice do PIB = log(PIBpercapita) – log100/log 40000 – log100
onde PIB per capita é o valor da renda per capita do país analisado, em dólar; U$40000 é o valor máximo de renda per capita no mundo. Um país que tenha o índice do PIB igual a 0,79, possui um PIB per capita aproximado de:
Dados: log 2 = 0,30; log 3 = 0,48; log5 =0,70
mar 17, 2007 @ 14:33:30
Sou Professor de Matemática no ensino secundário em Cabo verde.
relativamentes ás “bases especiais” de logarítmo há algumas confusões em livros diferentes: ums tratam log como logarítmo na base (e) e outros como base (10). Mas esses livros não trazem nenhuma nota para que os alunos possam se orientar.
o quê que é possível fazer para acabar com essa confusão?
mar 08, 2007 @ 17:37:11
Pô galera..site maneiro esse seuss..
=D
Gostei pakass…
bjo a todoss
mar 06, 2007 @ 09:39:04
preciso que me enviem toda matéria de logaritimo
fev 06, 2007 @ 11:42:59
Oi meu nome é mariana e estou com um trabalho para fazer de matematica e ele é sobre”por que todo o numero elevado a 0 e igual a um?” e eu nao sei.
por favor me ajudem!!!!!!!!!!
dez 20, 2006 @ 10:57:58
Olá!!
sou do 1 ano e nao so muito bom em matematica por isso peço ajuda a vcs do site.Gostaria de saber o resultado dessa questao:
log um meio x(x ao quadrado -5x+8)
dez 01, 2006 @ 10:49:25
Olá!
gostaria de saber qual seria a solução para a seguinte equação:
√x / x = log2 (10x) / √x
Obrigado
nov 22, 2006 @ 13:44:21
eu to apertada com um trabalho de matemática e to precisandu de uma conclusão geral sobre logaritmo, não to consegundo fazer…
Por favor me ajude senão vo me ferrar esse ano.
nov 07, 2006 @ 20:11:24
oi sou estudante de nutricao do segundo periodo e tenho uma duvida sobre uma conta de quimica
ph= -log 10 elevado a 2,32 : ph =-log 10 elevado a 2,11
tentei na calculadora cientifica mais nao consegui,ajudem me por favor se nao vou bombar na prova
out 31, 2006 @ 14:20:47
O q são Barras de Neper?
out 25, 2006 @ 10:46:38
as vossas dicas foram sensacional era oque eu estava esperando pra aprimorar meus conhecimentos de loga.valeu..basei=fuiii
out 09, 2006 @ 09:24:24
gostaria de saber quanto modos de logaltimo com bases diferentes e expoentes fiferente sera qui havera uma diferença nos ou nos expoents e e nos logalitimo se for impar,gradeceria q manda-se para meu email.
set 16, 2006 @ 18:11:25
Sou aluno da UTFPR, do curso de gestão de pequenas e médias empresas, estou fazendo uma pesquisa sobre logarítmos e gostaria de saber quais e quantas aplicações que os logarítmos têm. Se possível, passar também uma descrição mais detalhada de cada aplicação.
Grato pela atenção
e-mail para contato: o_noale@walla.com &
coringao_noale@hotmail.com
set 13, 2006 @ 14:35:10
Sou aluno do curso de Ciências Biloógicas da UFRPE e neste momento estou necessitando destes logaritmos neperianos :
. ln2,ln4,ln8, ln16,ln32,ln64
Agradeço.
Felipe
set 11, 2006 @ 14:51:56
como encontrar o valor do número de Euller utilizando as teclas de log na calculadora científica
set 04, 2006 @ 02:16:58
OI! EU ESTOU NO 2° ANO DO ENSINO MEDIO
E TENHO UMA DUVIDA RELACIONADO A LOGARITMOS
EX:LOG9 CUBICO RAIZ DE 27
ago 22, 2006 @ 23:38:33
Rogério,
Solução do item a):
log50,25 = log525.10-2 =
= log525 – 2log510
= 2 – (2log 10/log 5) = 2 – (2/0,6989) = 2 – 2,86 = -0,86
onde foram utilizadas algumas propriedades do logaritmo, a mudança para base 10 e cálculos aproximados.
O item b) deixo para você resolver :-)
ago 22, 2006 @ 19:18:51
Como posso resolver o seguinte problema?
Calcular os logaritmos em base 5 do números:
a) 0,25
b) 0,625
ago 15, 2006 @ 21:03:10
Ao estudar Logaritmo se percebe claramente que lidamos logo após com a função exponencial algo muito simples. bom vamos ao que interessa o conteudo apresentado neste site achei mto interessante, pois, mostra todas as propriedades logaritmicas alem de calculos auxiliares para casos especificos. a questao do anti-Log eu nao tinha conhecimento mas ao visitar tal site aprendi este caso. muito bom mesmo o conteudo deste site.
ago 03, 2006 @ 12:34:45
Tem um conteúdo magnífico, super claro e me ajudou muito Continue assim. Parabéns mesmo!!!
jul 05, 2006 @ 10:12:25
Foi de grande ajuda em meus estudos de calculo.
Tem grande conteudo, e sua explicação é totalmente clara
Meus parabens pela matéria
jun 01, 2006 @ 15:42:57
eu quero mto saber como se responde essa questão:
Uma pessoa deposita 5000 a 4% de juros. quanto ela tera apos 10 anos:
a)se os juros são pagos anualmente
b)se os juros são pagos trimestralmente
Viche » Equações Exponenciais
maio 30, 2006 @ 11:01:20
[…] Método que utiliza o conceito e propriedades de logaritmos. […]