Logaritmo foi o assunto escolhido, com 13 votos, na pesquisa realizada pelo VICHE. Para ver o resultado e os detalhes basta clicar no link Consultar Pesquisas localizado na barra lateral de navegação.
Antes de prosseguir com a abordagem do tema vencedor registro os nossos agradecimentos a todos os leitores participantes.
No artigo sobre equações exponenciais citamos os dois principais métodos utilizados para resolver este tipo de equação:
- o de redução a potências de mesma base, e
- o que utiliza o conceito e propriedades de logaritmos.
O primeiro foi tratado naquele artigo com a colocação de conceitos, exemplos e exercícios resolvidos, em que estes, foram propositalmente selecionados, visando apresentar o uso de técnicas diferenciadas na resolução de equações exponenciais.
O segundo será abordado agora, como já dito, com o intuito de auxiliá-lo a resolver equações do tipo 3x = 7, entre outras, em que não é possível reduzir seus termos a uma potência de mesma base.
Apesar de podermos afirmar com facilidade que x assume um valor entre 1 e 2, pois 3 < 3x = 7 < 9, não sabemos qual é exatamente esse valor e nem o processo para determiná-lo, tomando-se por base os conceitos publicados até aqui no VICHE.
Para isto é necessário acrescentar a seu repertório de conhecimentos a definição e propriedades dos logaritmos.
Definição
Dados a e b números reais e positivos, com a diferente de 1, definimos logaritmo de b na base a, o número x, cuja potência de grau x de a é igual a b. Ou seja:
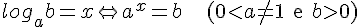
Observações e consequências da definição:
- Na expressão a esquerda a é denominado a base do logaritmo, b o logaritmando e x o logaritmo;
- Como a e b são ambos positivos e a é diferente de 1, existe um único valor de x que satisfaz a primeira igualdade na expressão acima;
- Decorre da definição de logaritmo que loga1 = 0, pois a0 = 1. Em outras palavras, que o logaritmo de 1 em qualquer base é igual 0;
- Do mesmo modo, observe que logaa = 1, uma vez que a potência de grau 1 de a é o próprio a. Ou seja, que o logarítmo da base, qualquer que seja a base satisfazendo, claro, as condições da definição, é igual a 1;
- Substituindo o valor de x da primeira igualdade na segunda, obtemos que alogab = b;
- logab = logac <=> b = c. Decorrência direta da definição (b = alogac) e do fato acima (alogac = c). Traduzindo: dois logaritmos em um mesma base são iguais se e somente se os logaritmandos são iguais;
- Note que de 6. pode-se afirmar, ainda, que em uma igualdade ao se aplicar o logaritmo aos seus membros essa igualdade não se altera;
- Ao conjunto de todos os logaritmos dos números reais positivos em uma base a (a > 0 e diferente de 1), denominamos de sistema de logaritmos de base a;
- Entre a infinidade de sistemas de logaritmos de base a, dois são particularmente importantes: o sistema de logaritmo decimais ou de base 10 e o sistema de logaritmo neperiano (também chamado de sistema de logaritmos naturais) ou de base e (e = 2,71828…, irracional);
- O logaritmo decimal é representado pela notação log10x ou simplesmente log x. E o neperiano por logex ou ln x;
- Fato histórico 1: Henry Briggs, Matemático Inglês (1561-1630) foi quem primeiro destacou a vantagem dos logaritmos de base 10, publicando a primeira tabela (ou tábua) de logaritmos de 1 a 1000 em 1617;
- Fato histórico 2: O nome neperiano vem de John Neper, Matemático Escocês (1550-1617), autor do primeiro trabalho publicado sobre a teoria dos logaritmos. O nome natural é devido ao fato de que no estudo dos fenômenos naturais geralmente aparece uma lei exponencial de base e.
Exemplos:
Antilogaritmo
Sejam a e b dois números reais positivos com a diferente de 1. Se o logaritmo de b na base a é igual a x, então b é o antilogaritmo de x na base a. Em símbolos:
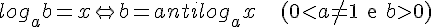
Exemplos:
Propriedades dos Logaritmos
L1. O logaritmo do produto de dois fatores reais e positivos em qualquer base a (a > 0 e diferente de 1) é igual a soma dos logaritmos dos fatores. Isto é:
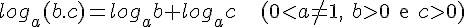
Demonstração:
Fazendo z = loga(b.c) temos, usando a definição de logaritmo, que:
az = b.c
Daqui, obtemos pela observação 5. acima:
az = alogab.alogac => az = alogab+logac => z = logab + logac
Substituindo z na última igualdade fica concluída a demonstração.
Uma outra forma, também simples e similar a anterior, de demonstrar a propriedade L1 é esboçada a seguir. Fazendo:
z = loga(b.c), x = logab e y = logac
vamos provar que z = x + y.
Aplicando a definição de logaritmo nas expressões acima obtemos, respectivamente:
az = bc, ax = b e ay = c
Substituindo b e c na primeira igualdade vem que:
az = axay => az = ax+y => z = x + y
A propriedade L1 é válida para o logaritmo do produto de n fatores (n > 2) reais e positivos, ou seja:
loga(b1.b2. … .bn) = logab1 + logab2 + … + logabn
A prova pode ser feita utilizando-se o método de indução sobre n, que consiste em:
- demonstrar que é verdadeira para n = 2 – já feita;
- supor que é válida para n = p > 2 e demonstrar que é verdadeira para n = p + 1.
Deixo para vocês a demonstração com a seguinte dica: agrupar como produto de dois fatores de modo a aplicar L1 e após utilizar a hipótese para n = p.
L2. O logaritmo do quociente de dois números reais e positivos em qualquer base a (a > 0 e diferente de 1) é igual ao logaritmo do dividendo menos o logaritmo do divisor nessa mesma base. Em símbolos:
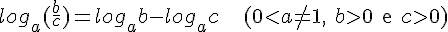
Demonstração:
De maneira semelhante à adotada na propriedade L1, fazendo z = loga(b/c) obtemos:
Como consequência direta da propriedade L2 temos que:
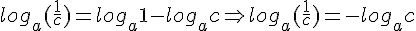
Cologaritmo
Dados a e b dois números reais positivos, com a diferente de 1, define-se cologaritmo de b na base a ao oposto do logaritmo de b nessa base a. Ou seja:
cologab = -logab = loga(1/b)
L3. O logaritmo da potência de grau x de b em qualquer base a (a, b reais positivos, x real e a diferente de 1) é igual ao produto do expoente x pelo logaritmo de b na base a. Em símbolos:
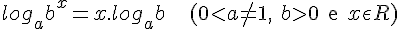
Demonstração:
Novamente fazemos uso do procedimento utilizado na demonstração das propriedades anteriores:
Fica como exercício a demonstração das propriedades L2 e L3 com o uso da segunda técnica adotada para provar a propriedade L1.
Como consequência da propriedade L3 temos que: o logaritmo da raiz de índice n de b na base a é igual ao produto do inverso do índice n pelo logaritmo do radicando na base a, i.e.:
![\Large log_a\sqrt[n]{b}=log_ab^{\frac{1}{n}}=\frac{1}{n}log_ab\hspace{20}(0\lt a\ne1\text{, }b\gt0\text{ e }n\epsilon N^*) \Large log_a\sqrt[n]{b}=log_ab^{\frac{1}{n}}=\frac{1}{n}log_ab\hspace{20}(0\lt a\ne1\text{, }b\gt0\text{ e }n\epsilon N^*)](http://www.blogviche.com.br/mimetex/pictures/bc4aab939c6ffc1a2d27eb3add4b3a10.gif)
Observações sobre as Propriedades L1, L2 e L3
- São válidas somente quando temos expressões logarítmicas que envolvam as operações de multiplicação, divisão e potenciação;
- Essas propriedades não permitem obter o logaritmo de uma soma ou diferença [loga(b + c) ou loga(b – c)]. Nestes casos, será necessário primeiro obter o valor da soma ou da diferença.
Mudança de Base
É muito comum, e você já deve ter se deparado com o fato, ter expressões ou equações logarítmicas em que seus membros estejam em bases diferentes.
Como na aplicação das propriedades operatórias, os logaritmos devem estar todos em uma mesma base é fundamental saber como isto é feito.
Você deve se lembrar (se não, volte às observações) que no início deste artigo mencionei como importante o sistema de logaritmo decimais ou de base 10, para o qual foi construída, pelo matemático Henry Briggs, uma tábua de logaritmos que possibilita determinar o seu valor para qualquer número real positivo.
Não abordaremos aqui os conceitos de mantissa e característica do logaritmo decimal utilizados para determinar seu valor com o auxílio da tabela. Fica apenas o registro de sua importância no uso das propriedades de mudança de base que apresentamos a seguir.
L4. Dados a, b e c números reais positivos, com a e c diferentes de 1, tem-se que:
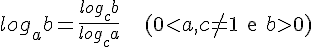
Demonstração:
Fazendo logab = x, logcb = y e logca = z provemos que x = y/z (note que z é diferente de zero, pois por definição a é diferente de 1). De fato:
Como consequência da propriedade L4 temos:
- logab = logcb.logac: a demonstração é feita transformando logcb para a base a no segundo membro da igualdade;
- logab = 1/logba: transforme logab para a base b.
Exercícios Resolvidos
1. Resolver a equação 3x = 7 (lembra-se, a do início do artigo):
Aplicando o logaritmo na base 10 aos dois membros da equação temos:
log 3x = log 7
Pela propriedade L3:
x.log 3 = log 7 => x = log 7/log 3 = 0,845/0,477 = 1,771
2. Um capital de R$50.000,00 foi aplicado a uma taxa de juros compostos de 5% ao ano, e o capital de R$45.000,00 a 6% ao ano. Em quanto tempo os montantes estarão iguais?
Um uso muito comum das propriedades de logaritmo para resolver equações exponencias é no cálculo de juros compostos cuja fórmula é:

onde M é o montante, C o capital, i a taxa de juros e t o tempo.
Solução:
Sejam M1 e M2 os montantes correspondentes aos capitais aplicados. Usando a fórmula, temos que:
M1 = 50000(1 + 0,05)t e M2 = 45000(1 + 0,06)t
Temos que determinar o tempo para que M1 = M2. Assim:
Referência:
- Fundamentos de Matemática Elementar, Gelson Iezzi, Osvaldo Dolce & Carlos Murakami, São Paulo, Atual Editora Ltda, edição 1977.
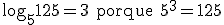
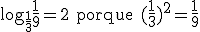
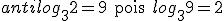
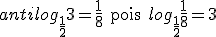



maio 28, 2010 @ 13:30:07
eu queria ajuda num trablho de matematica….
maio 04, 2010 @ 21:45:58
mesmo assim, nao sei calcular qlqr numero de log na base 10.
abr 29, 2010 @ 14:51:54
nossa vcs explicaram bem mas com a minha professora ANA CLAUDIA ficou mais facil!!!!!
abr 19, 2010 @ 13:12:11
Sera que voces podem ajudar-me a resolver este problema?
Poderia tambem, explicar-me como resolvo outros iguais?
Isto e parte do calculo de vasão de uma barrtagem.
1,78 x 0.60 x 0,018³/²
Meu email ta_aguirre@hotmail.com
Muito obrigado.
abr 18, 2010 @ 14:36:36
Poderiam ajudar-me aresolver este problema? Poderia exzplicar como resolvo outros iguais? 1,78 x 0.60 x 0,018³/²
Obrigado Aguirre
abr 12, 2010 @ 11:08:16
ola v6 estao de parabens mas gostaria de uma juda tem um exercicio que minha professora passou q fazendo ele com logaritmo apenas encontro o resultado 6 e resolvendo pela equção de segundo grau encontro o resultado 6 e 2 e ambos estão certo
é o seguinte exercicio log(x-3)elevado a 2 +log da raiz de 16=2logX
Gostaria que me falassem se ambas formas de fazer da certo , e se for correto pq deu resultados diferentes
nov 19, 2009 @ 19:17:00
continuei não entendendo nada?
out 27, 2009 @ 14:03:34
ta muito paia essa página,precisa de mais informações ;//
out 20, 2009 @ 13:20:06
o valor da igualdade :log9 3raíz de 27?
minha duvida.
ago 26, 2009 @ 15:48:15
muiiiito bom, gostaria de saber como fazer estas demonstracoes usando INTEGRAL, estou comecando uma iniciacao cientifica na disciplina e preciso dessa parte. Sou aluno da UFU Obrigado!!!
ago 13, 2009 @ 15:14:53
como resolvo estas equações:
20log.0,50dB = ?
20log.0,20dB = ?
ago 03, 2009 @ 09:28:51
logaritmos sao bem dificies de responder mais quando temos uma ajudinha como essa fik facil
jun 20, 2009 @ 18:39:46
LOG16 COM O EXPOENTE 2 RAIS DE 2=Y
maio 13, 2009 @ 09:13:20
Gostaria de saber como resolver um logaritimo que tem sua base elevada a um expoente?
Ex log²
2²
abr 23, 2009 @ 09:18:45
qual é a finalidade do logaritimo na pratica?
gostaria que me dacem materia de matemática e fisica mecânica
fev 08, 2009 @ 21:08:57
Pesquisei muito na net e não vi de que outra forma Briggs desenvolveu a tabela de logaritmos de base 10. Eu consegui.
jan 29, 2009 @ 09:49:53
quero saber sobre logaritmo neperiano
dez 29, 2008 @ 15:48:33
Bom, a explicação foi muito útil. Porém, preciso resolver um exercício urgente. Tenho pouca noção sobre o assunto pois acabo de ir para a 8ª série. Obrigada pela atenção.
dez 15, 2008 @ 04:00:59
preciso da tabela com valores das mantissas de logarítimos na base neperiana.
dez 01, 2008 @ 11:28:37
Primeiramente queria parabenizar o site, tem explicações clarar e objetivas. Simples de se entender.
Em segundo lugar queria poder esclarecer uma dúvida que não consegui tirar… meu professor passou um exercício e deu somente o resultado, pedindo para que nós mostrássemos a ele qual seria a forma correta para se chegar a esse resultado.
Pelo que vejo da operação é uma coisa muito simples, porém, não encontro meios de resolvê-la. Será que poderiam me ajudar?!
A operação é a seguinte: 10(base)log 5(expoente) x log7/5 (expoente) = 7.
Como podem ver o resultado é 7! Qual seria a maneira correta para se chegar a esse resultado?
nov 25, 2008 @ 18:20:46
Cade a tebela de briggs????
se voces postarem isso, ficarei muito agradecida!
obrigada!
nov 17, 2008 @ 09:22:07
Meu nome é gisleno e por favor estou sem saber o que fazer minha professora me padio 10 aplicações de logaritimos e ñ sei como fazer, vc pode me ajudar ? preciso muito por favor.
nov 01, 2008 @ 11:22:31
oimas dicas e respostas
out 29, 2008 @ 13:54:36
nao consigo resolver a equacao log2raizde8=x
out 13, 2008 @ 21:34:07
esse site nao presta
out 12, 2008 @ 11:52:09
como encontrar o log7
out 09, 2008 @ 22:26:21
— Queria saber o seguinteee
qual a propriedade disso: logaritimo com logaritmando e base com expoente…e logararito de base com expoente!!
out 08, 2008 @ 10:05:38
… fiquei maravilhado com a exaltidão com a qual foi abordado o tema referente às propriedades de logarítmos, e muito mais ainda pelas demonstrações apresentadas. Fantástico…
set 22, 2008 @ 16:08:57
me ajude pessoal se eu vo se fera
logaritimos e foda
ago 19, 2008 @ 18:22:20
Boa tarde! eu gostaria muito que vc’s me ajudacem a fazer Log, sei que naum é dificil, mais naum entra na minha cabeça!
Como por exemplos essas equações na qual tenho que determinar o conjunto de valores reais de X para que possivel definir, e naum sei nem por onde começar, Por Exemplo essas equações: LOGx-1(X+4), LOGx(X ao quadrado -4), LOGx+1(X ao quadrado -5+6).
Agradeço desde de já a ajuda!
ago 11, 2008 @ 22:47:50
– Explicação realmente é boa (:
eu gosteii sim , mas acho qê deviia
seer um pouco menoor & mais pratiica,
mas dá pra entendeer (y’
jul 02, 2008 @ 12:05:47
Como posso demonstrar geometricamente que a multiplição de dois números é igual a soma, ou seja, utilizando áreas como posso prova essa propriedade.
jun 26, 2008 @ 13:10:59
tenho uma duvida como resolver esta equações:
log(x)=5
3
log(3)=2
x
jun 18, 2008 @ 23:37:12
olá , gostaria de saber qual a solução para este problema :
y= ( -1 )^M + ( -1 )^M+1
aguardo , obrigado !
maio 28, 2008 @ 12:43:28
Estou no 1º Semestre de ADM, não estou entendendo de logaritimos, pois faz mtos anos que parei de estudar.
Me ajudem por favor!!!!!!
Obrigado!
abr 09, 2008 @ 22:10:05
Muito bom mesmo! Varri a internet atrás de uma boa explicação soobre logarítimos e aqui achei a melhor. Valeu mesmo, me ajudou muito nos meus estudos ;-)
abr 02, 2008 @ 14:59:33
muito bom..
mar 09, 2008 @ 16:37:31
matematica e um saco
da matematica o q ,q agente leva pro futuro ainda mais eu q quero ser pscicologa hem me diz por favor
fev 27, 2008 @ 14:00:22
aprendi logaritmo!
fev 27, 2008 @ 13:58:57
o site é melhor q a minha professora de matemática,pois é bem mais detalhado e específico,sem esse negócio de utilizar
borrão.
fev 21, 2008 @ 11:27:14
queria saber o logaritimo de 100
fev 09, 2008 @ 05:43:18
gostei do site tem coisas super interessantes q me vao ajudar muito para o texte de ingresso a faculdade.
dez 13, 2007 @ 10:11:58
qual e o logaritmo de 49 na base 7
nov 26, 2007 @ 16:57:23
gostei bastante
nov 22, 2007 @ 20:36:42
A grande maioria dos exercícios usa a propriedade dos logaritmos de forma correta, porém, quando chega no final, tomando por base um exercício que eu ví neste site, eles não explicam por exemplo como se calcula o log de 7 dividido pelo log de 3, eles ja colocam os valores calculados talvez na máquina científica e aí dão o resultado final, no caso 1,771. Como e que eu vou saber qual o log de 7, ou como é que eu vou saber que 10 elevado a x é igual a sete ou que 10 elevado a x é igual a 3, como é que eu vou saber o valor do ‘ x ‘.
nov 14, 2007 @ 00:51:16
Não sei como resolver logaritmos.Pode me explicar ?
responde com este ex:Log3 (2x + 7)
nov 08, 2007 @ 16:18:37
seu site é uma porcaria
nov 04, 2007 @ 19:02:56
eu queria ajuda num trabalho que eu nao consigo fazer de matematica
out 17, 2007 @ 22:58:36
gostaria de saber como se determina o conjunto de equção log2 (2x – 4)=4
e este também
sabendo que log2 =0,3 e log3=0,5 caucule log4 log27 log288
e aplicada a definição de logaritimo
log8 1
log9 __1__
243
po favor serei grata caso me ajudem reckomendarei aos meus colegas que os visite
agradeço desde já
out 14, 2007 @ 20:16:39
queria saber se vc’s poderiam me ajudar…
Eu gostaria de saber quais sao as aplicações dos logaritmos eu já revirei toda a web e ainda não encontrei nada gostaria de pedir a ajuda do super herois daí.Então pedido feito,espero alguma resposta. por favo me ajudem é pra um trabalho escolar…
Gabi
aguardando resposta…