Logaritmo foi o assunto escolhido, com 13 votos, na pesquisa realizada pelo VICHE. Para ver o resultado e os detalhes basta clicar no link Consultar Pesquisas localizado na barra lateral de navegação.
Antes de prosseguir com a abordagem do tema vencedor registro os nossos agradecimentos a todos os leitores participantes.
No artigo sobre equações exponenciais citamos os dois principais métodos utilizados para resolver este tipo de equação:
- o de redução a potências de mesma base, e
- o que utiliza o conceito e propriedades de logaritmos.
O primeiro foi tratado naquele artigo com a colocação de conceitos, exemplos e exercícios resolvidos, em que estes, foram propositalmente selecionados, visando apresentar o uso de técnicas diferenciadas na resolução de equações exponenciais.
O segundo será abordado agora, como já dito, com o intuito de auxiliá-lo a resolver equações do tipo 3x = 7, entre outras, em que não é possível reduzir seus termos a uma potência de mesma base.
Apesar de podermos afirmar com facilidade que x assume um valor entre 1 e 2, pois 3 < 3x = 7 < 9, não sabemos qual é exatamente esse valor e nem o processo para determiná-lo, tomando-se por base os conceitos publicados até aqui no VICHE.
Para isto é necessário acrescentar a seu repertório de conhecimentos a definição e propriedades dos logaritmos.
Definição
Dados a e b números reais e positivos, com a diferente de 1, definimos logaritmo de b na base a, o número x, cuja potência de grau x de a é igual a b. Ou seja:
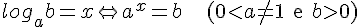
Observações e consequências da definição:
- Na expressão a esquerda a é denominado a base do logaritmo, b o logaritmando e x o logaritmo;
- Como a e b são ambos positivos e a é diferente de 1, existe um único valor de x que satisfaz a primeira igualdade na expressão acima;
- Decorre da definição de logaritmo que loga1 = 0, pois a0 = 1. Em outras palavras, que o logaritmo de 1 em qualquer base é igual 0;
- Do mesmo modo, observe que logaa = 1, uma vez que a potência de grau 1 de a é o próprio a. Ou seja, que o logarítmo da base, qualquer que seja a base satisfazendo, claro, as condições da definição, é igual a 1;
- Substituindo o valor de x da primeira igualdade na segunda, obtemos que alogab = b;
- logab = logac <=> b = c. Decorrência direta da definição (b = alogac) e do fato acima (alogac = c). Traduzindo: dois logaritmos em um mesma base são iguais se e somente se os logaritmandos são iguais;
- Note que de 6. pode-se afirmar, ainda, que em uma igualdade ao se aplicar o logaritmo aos seus membros essa igualdade não se altera;
- Ao conjunto de todos os logaritmos dos números reais positivos em uma base a (a > 0 e diferente de 1), denominamos de sistema de logaritmos de base a;
- Entre a infinidade de sistemas de logaritmos de base a, dois são particularmente importantes: o sistema de logaritmo decimais ou de base 10 e o sistema de logaritmo neperiano (também chamado de sistema de logaritmos naturais) ou de base e (e = 2,71828…, irracional);
- O logaritmo decimal é representado pela notação log10x ou simplesmente log x. E o neperiano por logex ou ln x;
- Fato histórico 1: Henry Briggs, Matemático Inglês (1561-1630) foi quem primeiro destacou a vantagem dos logaritmos de base 10, publicando a primeira tabela (ou tábua) de logaritmos de 1 a 1000 em 1617;
- Fato histórico 2: O nome neperiano vem de John Neper, Matemático Escocês (1550-1617), autor do primeiro trabalho publicado sobre a teoria dos logaritmos. O nome natural é devido ao fato de que no estudo dos fenômenos naturais geralmente aparece uma lei exponencial de base e.
Exemplos:
Antilogaritmo
Sejam a e b dois números reais positivos com a diferente de 1. Se o logaritmo de b na base a é igual a x, então b é o antilogaritmo de x na base a. Em símbolos:
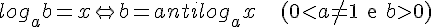
Exemplos:
Propriedades dos Logaritmos
L1. O logaritmo do produto de dois fatores reais e positivos em qualquer base a (a > 0 e diferente de 1) é igual a soma dos logaritmos dos fatores. Isto é:
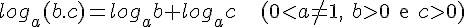
Demonstração:
Fazendo z = loga(b.c) temos, usando a definição de logaritmo, que:
az = b.c
Daqui, obtemos pela observação 5. acima:
az = alogab.alogac => az = alogab+logac => z = logab + logac
Substituindo z na última igualdade fica concluída a demonstração.
Uma outra forma, também simples e similar a anterior, de demonstrar a propriedade L1 é esboçada a seguir. Fazendo:
z = loga(b.c), x = logab e y = logac
vamos provar que z = x + y.
Aplicando a definição de logaritmo nas expressões acima obtemos, respectivamente:
az = bc, ax = b e ay = c
Substituindo b e c na primeira igualdade vem que:
az = axay => az = ax+y => z = x + y
A propriedade L1 é válida para o logaritmo do produto de n fatores (n > 2) reais e positivos, ou seja:
loga(b1.b2. … .bn) = logab1 + logab2 + … + logabn
A prova pode ser feita utilizando-se o método de indução sobre n, que consiste em:
- demonstrar que é verdadeira para n = 2 – já feita;
- supor que é válida para n = p > 2 e demonstrar que é verdadeira para n = p + 1.
Deixo para vocês a demonstração com a seguinte dica: agrupar como produto de dois fatores de modo a aplicar L1 e após utilizar a hipótese para n = p.
L2. O logaritmo do quociente de dois números reais e positivos em qualquer base a (a > 0 e diferente de 1) é igual ao logaritmo do dividendo menos o logaritmo do divisor nessa mesma base. Em símbolos:
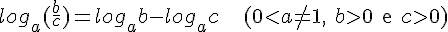
Demonstração:
De maneira semelhante à adotada na propriedade L1, fazendo z = loga(b/c) obtemos:
Como consequência direta da propriedade L2 temos que:
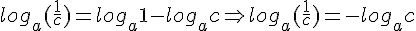
Cologaritmo
Dados a e b dois números reais positivos, com a diferente de 1, define-se cologaritmo de b na base a ao oposto do logaritmo de b nessa base a. Ou seja:
cologab = -logab = loga(1/b)
L3. O logaritmo da potência de grau x de b em qualquer base a (a, b reais positivos, x real e a diferente de 1) é igual ao produto do expoente x pelo logaritmo de b na base a. Em símbolos:
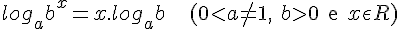
Demonstração:
Novamente fazemos uso do procedimento utilizado na demonstração das propriedades anteriores:
Fica como exercício a demonstração das propriedades L2 e L3 com o uso da segunda técnica adotada para provar a propriedade L1.
Como consequência da propriedade L3 temos que: o logaritmo da raiz de índice n de b na base a é igual ao produto do inverso do índice n pelo logaritmo do radicando na base a, i.e.:
![\Large log_a\sqrt[n]{b}=log_ab^{\frac{1}{n}}=\frac{1}{n}log_ab\hspace{20}(0\lt a\ne1\text{, }b\gt0\text{ e }n\epsilon N^*) \Large log_a\sqrt[n]{b}=log_ab^{\frac{1}{n}}=\frac{1}{n}log_ab\hspace{20}(0\lt a\ne1\text{, }b\gt0\text{ e }n\epsilon N^*)](http://www.blogviche.com.br/mimetex/pictures/bc4aab939c6ffc1a2d27eb3add4b3a10.gif)
Observações sobre as Propriedades L1, L2 e L3
- São válidas somente quando temos expressões logarítmicas que envolvam as operações de multiplicação, divisão e potenciação;
- Essas propriedades não permitem obter o logaritmo de uma soma ou diferença [loga(b + c) ou loga(b – c)]. Nestes casos, será necessário primeiro obter o valor da soma ou da diferença.
Mudança de Base
É muito comum, e você já deve ter se deparado com o fato, ter expressões ou equações logarítmicas em que seus membros estejam em bases diferentes.
Como na aplicação das propriedades operatórias, os logaritmos devem estar todos em uma mesma base é fundamental saber como isto é feito.
Você deve se lembrar (se não, volte às observações) que no início deste artigo mencionei como importante o sistema de logaritmo decimais ou de base 10, para o qual foi construída, pelo matemático Henry Briggs, uma tábua de logaritmos que possibilita determinar o seu valor para qualquer número real positivo.
Não abordaremos aqui os conceitos de mantissa e característica do logaritmo decimal utilizados para determinar seu valor com o auxílio da tabela. Fica apenas o registro de sua importância no uso das propriedades de mudança de base que apresentamos a seguir.
L4. Dados a, b e c números reais positivos, com a e c diferentes de 1, tem-se que:
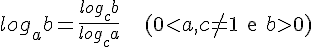
Demonstração:
Fazendo logab = x, logcb = y e logca = z provemos que x = y/z (note que z é diferente de zero, pois por definição a é diferente de 1). De fato:
Como consequência da propriedade L4 temos:
- logab = logcb.logac: a demonstração é feita transformando logcb para a base a no segundo membro da igualdade;
- logab = 1/logba: transforme logab para a base b.
Exercícios Resolvidos
1. Resolver a equação 3x = 7 (lembra-se, a do início do artigo):
Aplicando o logaritmo na base 10 aos dois membros da equação temos:
log 3x = log 7
Pela propriedade L3:
x.log 3 = log 7 => x = log 7/log 3 = 0,845/0,477 = 1,771
2. Um capital de R$50.000,00 foi aplicado a uma taxa de juros compostos de 5% ao ano, e o capital de R$45.000,00 a 6% ao ano. Em quanto tempo os montantes estarão iguais?
Um uso muito comum das propriedades de logaritmo para resolver equações exponencias é no cálculo de juros compostos cuja fórmula é:

onde M é o montante, C o capital, i a taxa de juros e t o tempo.
Solução:
Sejam M1 e M2 os montantes correspondentes aos capitais aplicados. Usando a fórmula, temos que:
M1 = 50000(1 + 0,05)t e M2 = 45000(1 + 0,06)t
Temos que determinar o tempo para que M1 = M2. Assim:
Referência:
- Fundamentos de Matemática Elementar, Gelson Iezzi, Osvaldo Dolce & Carlos Murakami, São Paulo, Atual Editora Ltda, edição 1977.
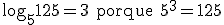
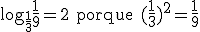
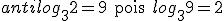
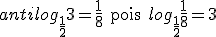



abr 29, 2013 @ 23:01:20
gostaria q vcs m ajudassem a resolver est questao 81 1,243=x
out 27, 2012 @ 18:54:30
EU QUERIA A TABUADA TODA E NO SAITE SO TEM A METADE
out 09, 2011 @ 13:51:27
preciso de ajuda
jun 14, 2011 @ 13:19:34
oII gostaria de saber se vc pode me ajedar em algumas questões de logaritimos que meu profesor passou.. e eu não consigo faser???
abr 25, 2011 @ 21:32:43
A bula de certo Medicamento informa que, a cada seis horas apôs Sua ingestão, metade dele é absorvida pelo organismo. se uma pessoa tomar 200 mg desse medicamento, quanto ainda restará a ser absorvido pelo organismo imediatamente após 18 horas de sua ingestão? E após ”t” horas?
fev 07, 2011 @ 15:44:19
gostaria q vcs me ajudassem a resolver essa questão
log 8 = a entao log ∛2 VALE:
jun 30, 2011 @ 20:07:06
Temos que ∛2 = 2^1/3 (usando o ^ pra elevado, por ex.: 3^2 = 3²). Então, fica: log2^1/3 = 1/3*log 2 (1).
Temos também que 8 = 2³. Então: log 8 = log 2³ = 3*log 2 = a. Dividindo por 3 em ambos os lados temos: log 2 = a/3. Substituindo o log 2 em (1), vem: 1/3*a/3 = a/9.
Não sei se fiz certo, espero ter ajudado.
jan 26, 2011 @ 17:17:18
gostaria que resolvesse essa questão: A produção de açai,em certa localidade do Marajó, era de X toneladas no ano 2000. A partir desse ano,a produção dobrou a cada ano.Após quanto tempo a produção passou a ser igual a 10 vezes a do ano 2000?
(dado:log 2 =0,30)
A) 2 ANOS E 4 MESES
B) 3 ANOS E 2 MESES
C)3 ANOS E 4 MESES
D)4 ANOS E 2 MESES
E)5 ANOS E 3 MESES
MANDE-ME A RESOLUÇÃO DESSA QUESTÃO DO IFPA..
nov 23, 2010 @ 20:57:08
pow ta muito dificil isso
out 21, 2010 @ 15:09:01
eu gostaria que tivesse mais calculos díficeis e explicativos…
out 21, 2010 @ 15:07:28
eu gostaria que tivesse mais calculos díficeis como exemplos e bem mais explicados…
set 17, 2010 @ 11:13:17
Bom pra começar ,os logaritmos devemos usar em casos de propriedade em logaritmando.
como por exemplo:logaritmo do produto.logaritmo do quociente,logaritmo da potencia
ago 23, 2010 @ 08:20:15
tenho muitas duvidas a cerca dos logaritimos pesso ajuda de todas as forrmulas obrigado pela compressao adeus
jul 07, 2010 @ 21:48:56
log2(x-1)(x-2)=1 Qual é o resultado?
jun 24, 2010 @ 15:00:41
gostaria q resolvesse esta conta log5 0,000064
abr 01, 2012 @ 14:05:24
Resultado R: (-1/6)
Símbolos usados para melhor entendimento do exercício
<- Implica
^ <- Elevado ou seja o nosso expoente
Resolução
log5 0,000064 <- 0,000064^X = 5
Transformando a dizima em facção 0,000064 = (64/1.000.000)
(64/1.000.000)= 5 <- (2/10)^6X = 5
Usando a regra de potencia (A/B)^n =(B/A)^-n
(10/2)^-6X=5 <- (5)^-6X=5
Bases iguais ignoramos as bases e trabalhamos como os expoentes
-6X=1 <- x=(-1/6)
jun 10, 2010 @ 16:26:08
Como fazer log(-8) na base 2
maio 31, 2010 @ 14:17:42
Como claculo LOG 5 NA BASE 2?
obrigado