Em continuidade ao artigo Progressões – Parte I que trata dos conceitos e propriedades de sequência e da Progressão Aritmética (PA), vamos, agora, fazer a abordagem teórica sobre as Progressões Geométricas (PG).

Progressões Geométricas (PG)

Definição

Uma progressão geométrica (PG) é uma sequência numérica em que cada termo, a partir do segundo, é igual ao antecessor multiplicado por uma constante q denominada a razão da PG. Ou seja:

an = an-1.q (n >= 2)

Observe que se a1 e q são diferentes de zero podemos escrever q = an/an-1, uma vez que, nessas condições, todos os termos da PG são também diferentes de zero.

Exemplos:

  1. (1; 2; 4; 8; 16; …) onde a1 = 1 e q = 2;
  2. (-2; -6; -18; -54; …) onde a1 = -2 e q = 3;
  3. (9; 9; 9; 9; …) onde a1 = 9 e q = 1;
  4. (1; -3; 9; -27; …) onde a1 = 1 e q = -3;
  5. (20; 0; 0; 0; …) onde a1 = 20 e q = 0.

Classificação

As PG são classificadas em cinco categorias de acordo com os valores do seu primeiro termo a1 e de sua razão q.

a) Crescentes:

São as PG em que cada termo é maior do que o seu antecessor (exemplo 1. acima) e ocorre nas duas situações seguintes:

  1. a1 > 0 e q > 1 (termos positivos e razão maior do que 1);
  2. a1 < 0 e 0 < q < 1 (termos negativos e a razão entre zero e um).

Demonstração de 1:

Como a1 e q são diferentes de zero, temos

an/an-1 = q > 1 <==> an > an-1

b) Decrescentes

São as PG em que cada termo é menor do que o seu antecessor (exemplo 2.) e ocorre nas duas situações abaixo indicadas:

  1. a1 < 0 e q > 1 (termos negativos e razão maior do que 1);
  2. a1 > 0 e 0 < q < 1 (termos positivos e a razão entre zero e um).

c) Constantes

São as PG em que cada termo é igual ao anterior (exemplo 3.):

  1. a1 = 0 e q qualquer;
  2. a1 = c e q = 1, onde c é um número real qualquer.

d) Alternantes

São as PG em que cada termo tem o sinal contrário ao de seu antecessor (exemplo 4.). Ocorre quando q < 0 e a1 é diferente de zero.

e) Estacionárias

São as PG em que seu termo inicial a1 é diferente de zero e todos os demais são iguais a zero (exemplo 5.). Ocorre quando q = 0, e, claro, a1 é diferente de zero.

Fórmula do Termo Geral de uma PG

Seja (a1; a2; a3; … ; an-1; an; …) uma PG de razão q, então seu enésimo termo (an) é:

an = a1.qn-1

Demonstração:

Pelo princípio da indução finita:

i) Verdadeira para n = 1:

a1 = a1.q1-1 => a1 = a1.qo = a1.1 = a1

ii) Suponhamos que a fórmula é verdadeira para n = p (hipótese da indução) e mostremos que é verdadeira para n = p + 1, isto é:

ap = a1.qp-1 => ap+1 = a1.qp+1-1 = a1.qp

Da definição de PG:

ap+1 = ap.q

Da hipótese, vem:

ap+1 = a1.qp-1.q => ap+1 = a1.qp+1-1 = a1.qp

Interpolação Geométrica

Interpolar k meios geométricos entre dois números a e b, é o mesmo que determinar uma PG de n = k + 2 termos, onde seus extremos sejam iguais a esses números, ou seja, onde a1 = a e an = b.

Como temos os extremos definidos, para interpolar meios em uma PG basta calcular sua razão. Assim, da definição de PG temos:

\LARGE a_n = a_1.q^{n-1}\Rightar b = a.q^{k+1}\Rightar q = \sqrt[k+1]{\frac{b}{a}}

Note que se o índice da raiz é par, teremos como solução duas PG distintas correspondente a q positivo e q negativo, respectivamente.

Soma dos Termos de uma PG Finita

A soma dos n primeiros termos de uma PG é:

\LARGE S_n = \frac{a_1(q^n-1)}{q-1}\hspace{3}(q\ne1)

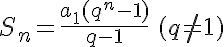
Demonstração:

Temos:

Sn = a1 + a2 + a3 + … + an-1 + an

Multiplicando os membros da igualdade por q obtemos

qSn = a1q + a2q + a3q + … + an-1q + anq = a2 + a3 + … + an + an+1

Na última passagem foi utilizada a definição de PG. Subtraindo membro a membro esta igualdade da anterior e cancelando os termos comuns:

qSn – Sn = -a1 + an+1 = -a1 + a1.qn

Colocando Sn e a1 em evidência vem:

(q – 1)Sn = a1(qn – 1)

Dessa última igualdade se obtem a fórmula da soma.

Soma dos Termos de uma PG Infinita (Limite da Soma)

Inicialmente, deixemos claro que a fórmula da soma a seguir só se aplica quando -1 < q < 1. Isto porque, somente nessas condições, uma PG infinita converge, ou seja, à medida que n tende para infinito, qn tende a zero.

Caso contrário, quando q > 1 ou q < -1, qn cresce indefinidamente à medida que n cresce, e, portanto, é impossível calcular a soma dos termos da PG. Lembre-se que em uma PG seus termos crescem ou decrescem em função da razão.

Para clarear, tome como exemplo a PG infinita definida por:

\LARGE (\frac{1}{2},\frac{1}{4},\frac{1}{8},\cdots,\frac{1}{2^n},\cdots)

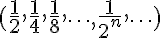
cuja soma dos seus n primeiros termos, aplicando-se a fórmula é (deixo os cálculos para você):

Soma de uma PG Finita

Conforme n aumenta indefinidamente (na fração) o seu denominador aumenta da mesma forma e, em consequência, a fração assume valores cada vez mais próximos de zero e Sn se aproxima de 1. Ou seja:

Limite da Soma

Dessa forma, podemos agora estabelecer a definição da soma dos termos de uma PG infinita.

Seja (a1; a2; a3; … ; an-1; an; …) uma PG infinita de razão q, -1 < q < 1, então a soma de seus termos é dada por:

Fórmula da Soma de uma PG infinita

Demonstração:

Como em Sn, qn tende a zero quando n tende a infinito temos:

Demonstração da Soma de uma PG Infinita

Referências:

  1. Fundamentos de Matemática Elementar, Gelson Iezzi, Osvaldo Dolce & Carlos Murakami, São Paulo, Atual Editora Ltda, edição 1977;
  2. Matemática para o Ensino Médio: Volume Único, Manoel Jairo Bezerra, São Paulo, Editora Scipione, 2001.

Nenhum artigo relacionado.