Viche

Exercícios Resolvidos #3 - Radiciação

julho 29th, 2006

Exercícios resolvidos sobre Radiciação com o objetivo de fixar os conceitos e as propriedades já tratadas no artigo de mesmo nome. Inicia com a questão do leitor identificado como HENRIQUE (comentário #33) sobre raiz de índice m da raiz de índice n ou como dito por ele, radical duplo.

Em seguida, serão resolvidos outros exercícios em que procuro cobrir todas as propriedades esboçadas no texto teórico acima mencionado. Em caso de dúvidas leia o artigo cujas propriedades serão aqui apenas assinaladas por P1, P2, …, P7 quando usadas.

Exercício 1: A raiz de índice m de uma raiz de índice n de a é igual à raiz de índice mn de a:

O que a propriedade diz? Diz que o resultado é o mesmo se você calcula a raiz de índice n de a e depois a raiz de índice m do valor obtido dessa operação ou se você calcula, diretamente, a raiz de índice mn de a. Faça esses cálculos com a raiz cúbica da raiz quadrada de 64 e a raíz sexta de 64, e veja que o resultado obtido é igual a 2 em ambos os casos.

Solução 1:

Primeiro, lembro a seguinte propriedade de potenciação: em uma igualdade ao se elevar ambos os seus membros à uma potência de grau m ela não se altera. Desse fato e supondo que:

vem (elevando ambos os membros à potência m) que:

e pela definição de radiciação:

o que conclui a demonstração.

Solução 2:

Uma outra maneira de demonstrar a propriedade (P5) é através da aplicação da propriedade P7:

Exercício 2: Calcular

Solução:
Para facilitar a explicação, e consequentemente o entendimento, vamos, inicialmente, tratar separadamente cada membro da expressão, onde se indicam as propriedades utilizadas em cada passagem:

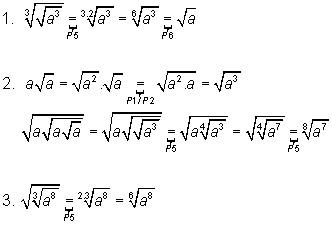
Assim de 1, 2 e 3 obtemos:

Exercício 3: (UFCE) Simplificar a expressão:

Solução:

Exercício simples que se baseia na decomposição em fatores primos de cada radicando e da utilização da propriedade P1, como você pode observar no detalhamento a seguir. Tenha em conta que na soma ou subtração de radicais, cada parcela deve ser considerada isoladamente para se obter o resultado de uma expressão. Ou seja, não se aplica que a soma de duas raízes de mesmo índice é igual a raiz da soma, como é o caso do produto, por exemplo.

Exercício 4: Calcular o quociente:

Solução:

Outro exercício de solução simples onde demonstro o uso das propriedades P1 e P3, e novamente, faço uso da decomposição em fatores primos dos radicandos:

Exercício 5: Escrever em ordem de grandeza crescente os radicais:

Solução:

Para fazer a comparação entre os radicais devemos, inicialmente, reduzí-los ao mesmo índice. Isto é feito calculando o mínimo múltiplo comum (mmc) dos índices e, após, aplicando a propriedade P6. O mmc(2, 4, 3, 6) = 12 e reescrevendo os radicais (P6) vem:

Agora, basta considerar a ordem dos radicandos para estabelecer a ordem crescente dos radicais:

Exercício 6: Efetuar

Solução:

Esboçada a seguir, onde utilizamos o fato de que o produto da soma pela diferença de dois números é igual ao quadrado do primeiro menos o quadrado do segundo (produto notável - PN) e as propriedades da Radiciação indicadas:

Artigos Relacionados:

• Questionarious #1 - Potenciação e Radiciação
• Radiciação

Categorias: Matemática, Questionarious/Exercícios Resolvidos, Técnico

89,190 Views