Matematica feeds

Frações: Operações – Parte III

outubro 12th, 2007

Adição

É a operação que tem por fim determinar uma fração que contenha todas as unidades e partes de unidades de várias parcelas de mesma natureza.

Entende-se por mesma natureza as frações que exprimem as mesmas partes da unidade, ou seja, que tenham o mesmo denominador, também conhecidas como homogêneas (2/8, 3/8 e 5/8 é um exemplo de tais frações).

Distinguem-se três casos na adição de frações.

A1. Soma ou adição de frações homogêneas ou de mesmo denominador.

Como fazer – Somam-se os numeradores e conserva-se o denominador comum.

Exemplo:

\frac{2}{8}+\frac{3}{8}=\frac{2 + 3}{8}=\frac{5}{8}

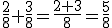
Como o denominador representa em quantas partes a unidade foi dividida, lembram-se, basta, para obter o número das partes, somar os numeradores.

Na figura a seguir temos uma pizza – prato comum em Brasília – servida para você e um amigo dividida em oito partes iguais (faça um esforço!). Se você come dois pedaços e seu amigo três, os dois juntos consumiram cinco partes em oito, ou seja, cinco oitavos da pizza.

Adição

A2. Adição de frações que não têm o mesmo denominador comum (frações heterogêneas).

Inicialmente, atente que não podemos somar quantidades de “coisas” diferentes e expressar o resultado em uma dessas “coisas”. Clareando: não podemos somar 5 maçãs e 3 bananas e dizer que o resultado é 8 maças ou 8 bananas.

Assim para somar frações heterogêneas é necessário, primeiro, transformar cada parcela nas mesmas partes da unidade, isto é, em frações que tenham o mesmo denominador comum.

Em resumo:

Como fazer – Para somar frações que não tenham o mesmo denominador, é preciso reduzi-las ao mesmo denominador e aplicar, então, a regra do primeiro caso A1.

Exemplo: Somar as frações 2/3, 5/8 e 1/6.

Utilizando-se da regra 2 de redução de frações ao mesmo denominador comum (veja a Parte II), temos que o mmc(3,6,8) = 24 e:

\frac{2}{3}+\frac{5}{8}+\frac{1}{6}=\frac{16}{24}+\frac{15}{24}+\frac{4}{24}=\frac{16+15+4}{24}=\frac{35}{24}

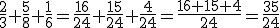
A3. Somar números mistos.

Como fazer:

  • Método 1: Para somar números mistos, somam-se primeiro as partes fracionárias, depois as partes inteiras, acrescentando-lhes também os inteiros obtidos na adição das partes fracionárias;
  • Método 2: Para somar números mistos, reduza-os, primeiro, a frações impróprias e após proceda como no caso A2.

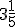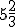Exemplo: Somar os números mistos 3\frac{1}{5} e 5\frac{2}{3}, pelo método 1. E você resolve pelo método 2, ok :-).

Pelo dito no método 1, temos:

3\frac{1}{5}+5\frac{2}{3}=3+5+\frac{1}{5}+\frac{2}{3}=8+\frac{3+10}{15}=8\frac{13}{15}=\frac{133}{15}

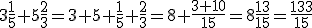
Subtração

É a operação que tem por objetivo tirar de um número dado todas as unidades e partes da unidade de outro número de mesma natureza.

Observação: No que se segue não serão considerados os casos em que o minuendo é menor do que o subtraendo, pois requer o conhecimento da teoria dos números relativos. Mas as regras em si permanecem válidas para quem é detentor do assunto.

Da mesma forma que na adição temos três casos que se distinguem na subtração.

S1. Subtração de duas frações com o mesmo denominador.

Como fazer – Subtrai-se o numerador da menor do numerador da maior e conserva-se o denominador comum.

Exemplo:

\frac{7}{12}-\frac{5}{12}=\frac{7-5}{12}=\frac{2}{12}=\frac{1}{6}

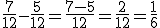
S2. Subtração de duas frações que não têm o mesmo denominador.

Lembrem-se, como colocado para a adição, que somente podemos subtrair quantidades de mesma natureza.

Como fazer – Da mesma forma que na adição, para se obter a subtração de frações heterogêneas, é preciso, primeiro, reduzi-las ao mesmo denominador, e, então, aplicar o caso S1.

Exemplo:

\frac{6}{7}-\frac{2}{5}=\frac{30}{35}-\frac{14}{35}=\frac{30-14}{35}=\frac{16}{35}

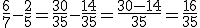
S3. Subtração de números mistos

  • Método 1: Para subtrair dois números mistos, subtraem-se primeiro as partes fracionárias, depois as partes inteiras e somam-se os resultados;
  • Método 2: Para subtrair dois números mistos, reduza-os, primeiro, a frações impróprias e após proceda como no caso S2.

Exemplo (método 2): Convertendo os números mistos dados na subtração para frações impróprias:

9\frac{2}{3}-2\frac{3}{5}=\frac{(9\times3)+2}{3}-\frac{(2\times5)+3}{5}=\frac{29}{3}-\frac{13}{5}

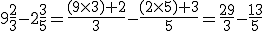
E reduzindo ao mesmo denominador comum – mmc(3,5)=15:

9\frac{2}{3}-2\frac{3}{5}=\frac{145}{15}-\frac{39}{15}=\frac{145-39}{15}=\frac{106}{15}

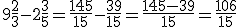
Multiplicação

A multiplicação de frações é a operação na qual partindo-se de duas frações dadas se obtem uma terceira que corresponde ao produto das duas anteriores.

M1. Multiplicar uma fração por outra.

Como fazer. Para se multiplicar uma fração por outra, multiplicam-se seus numeradores para obter o numerador da fração produto e seus denominadores para obter o denominador da fração produto.

Exemplo:

\frac{3}{8}\times\frac{5}{9}=\frac{3\times5}{8\times9}=\frac{15}{72}=\frac{5}{24}

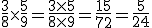
Observação: Para se multiplicar um inteiro por uma fração ou uma fração por um inteiro basta multiplicar esse inteiro pelo numerador da fração ou o numerador da fração por esse inteiro. É só notar que um numero inteiro pode ser representado por uma fração cujo denominador é um, por exemplo, 5 = 5/1, e chegamos no caso M1, em que o denominador não se altera uma vez que é multiplicado por um.

M2. Produto de várias frações: É o resultado obtido multiplicando a primeira fração pela segunda; depois este produto pela terceira, e assim sucessivamente, até a última fração.

Observe que o produto de frações se faz da mesma forma que o produto de números inteiros e que o resultado, no caso das frações, é obtido pela aplicação repetida do caso M1.

Como fazer – Multiplicam-se os numeradores entre si para obter o numerador do produto e os denominadores entre si para obter o denominador do produto.

Exemplo:

\frac{2}{5}\times\frac{3}{8}\times\frac{5}{6}=\frac{2\times3\times5}{5\times8\times6}=\frac{30}{240}=\frac{1}{8}

Os cálculos acima poderiam ser simplificados, suprimindo-se os fatores comuns ao numerador e ao denominador, antes de efetuá-los, como indicado a seguir:

\frac{2}{5}\times\frac{3}{8}\times\frac{5}{6}=\frac{\not2^1\times\not3^1\times\not5^1}{\not5_1\times\not8_4\times\not6_2}=\frac{1\times1\times1}{1\times4\times2}=\frac{1}{8}

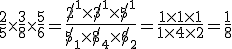
Divisão

Divisão de frações é a operação que tem por fim, dadas duas frações, dividendo e divisor, achar uma terceira, o quociente, tal que multiplicada pelo divisor, reproduza o dividendo.

D1. Dividir uma fração por um inteiro

Como fazer – Para se dividir uma fração por um inteiro multiplica-se o denominador pelo iinteiro.

Exemplo:

\frac{5}{6}\div3=\frac{5}{6\times3}=\frac{5}{18}

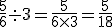
D2. Dividir um inteiro por uma fração.

Como fazer – Multiplica-se o inteiro pela fração invertida.

Exemplo:

5\div\frac{7}{3}=5\times\frac{3}{7}=\frac{5\times3}{7}=\frac{15}{7}

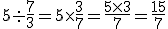
D3. Dividir uma fração por outra.

Como fazer – Multiplica-se a fração do dividendo pela fração do divisor invertida. Em outras palavras conserva-se a primeira (dividendo) e multiplica-se pelo inverso da segunda (divisor).

Exemplo:

\frac{\frac{3}{5}}{\frac{4}{7}}=\frac{3}{5}\div\frac{4}{7}=\frac{3}{5}\times\frac{7}{4}=\frac{3\times7}{5\times4}=\frac{21}{20}

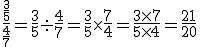
Observações Finais

  • O inverso de um número é o quociente de 1 por este número. Exemplos: o inverso de 2 é 1/2, o inverso de 3/5 é 5/3 e o de 1/5 é 5;
  • Duas frações são inversas quando o numerador de cada uma é o denominador da outra;
  • Quando duas frações têm o mesmo denominador, o quociente entre elas é igual à fração formada pelo numerador da primeira sobre o da segunda. Exemplo (1/5):(3/5) = 1/3;
  • O produto de dois números inversos é sempre 1;
  • Dois números são recíprocos quando o seu produto é igual à unidade.

Referências:

Elementos de Aritmética, Curso Superior – Para o curso colegial e admissão às escolas superiores, do Irmão Isidoro Dumont, Coleção de Livros Didáticos F. T. D, publicado em 26/10/1945.

Artigos Relacionados:

  1. Frações: Redução – Parte II
  2. Frações – Parte I
  3. Conjuntos: Operações – Parte II
  4. Conjuntos: Noções Básicas – Parte I
  5. Progressões – Parte II
  6. Progressões – Parte I
  7. Frações Irracionais e Racionalização

Posts relacionados trazidos a você pelo Yet Another Related Posts Plugin.

Categorias: Matemática,Técnico

Imprima este artigo Envie este artigo para um(a) amigo(a) Adicionar ao Rec6 Adicionar ao del.icio.us Adicionar ao Linkk 80.245 views

75 Comentários Adicione o seu

  • 1. gustavo&hellip  |  dezembro 3rd, 2007 at 20:22:29

    adorei esse site ele melivrou da pesquisa rs amen

  • 2. juscileia&hellip  |  dezembro 13th, 2007 at 15:04:07

    gostaria q explicasse melhor

    pois adoro matematima mais tenho dificudades

    estou fazendo trabalho d dependencia

    e ñ sei como fazer

    meu nome e juscilia
    moro em brasilia df

  • 3. RaQuEl&hellip  |  dezembro 17th, 2007 at 15:03:05

    é muito dificil matematica,eu odeio matematica
    vo bomba por causa di matematica
    pq………….:( issU matA Um

  • 4. Deyse&hellip  |  março 31st, 2008 at 20:03:38

    Adorei muito mesmo. Na realidade já sou apaixonada por matemática, ainda mais agora…

  • 5. larysssa oliveira&hellip  |  abril 7th, 2008 at 20:32:01

    eu adorei esse esclarecimento!
    me ajudou num trabalho de matemática super difícil!
    meus parabéns a vcs q fizeram esse site
    muito obrigado

  • 6. manuela dos santos garcia&hellip  |  abril 8th, 2008 at 16:31:58

    gostei muito desse site aprendi muito

  • 7. Rafael&hellip  |  abril 12th, 2008 at 16:53:35

    gostei muito ñ gostava muito de matematica mais agora passei a gostar

  • 8. clarissa sousa&hellip  |  abril 15th, 2008 at 19:06:53

    eu amo matematica

  • 9. Dario&hellip  |  abril 22nd, 2008 at 14:36:42

    1
    —————- ???????????????????
    1 + 2
    —
    2

  • 10. carlos roberto&hellip  |  abril 29th, 2008 at 19:58:35

    matematica é uma delicia infelismente agente so aprende quando fica velho, pois quando novo a cabeça esta no programa que vai passar na televisão e ai é onde o bicho pega, e quem leva a culpa e o professor, errado, a culpa é do aluno

  • 11. guilherme&hellip  |  maio 14th, 2008 at 18:55:16

    Muito abrigado vc me ajudou muito no trabalho de matemática =)

  • 12. diego henrique&hellip  |  maio 14th, 2008 at 20:38:54

    devia ter mais exemplos!!!

  • 13. letícia&hellip  |  maio 19th, 2008 at 17:05:32

    acabei indo bem na prova de matemática!!!

  • 14. luciana&hellip  |  maio 28th, 2008 at 01:43:18

    eu nao sei muito matemática mas acho uma otima ideia ter estas explicaçoes … …..

  • 15. Tiago&hellip  |  junho 3rd, 2008 at 13:37:33

    muito útil para desenrrascar enquanto se estuda.

  • 16. maria eduarda&hellip  |  junho 16th, 2008 at 20:26:27

    Matemática é muito bom.Eu gosto muito da matemática porque eu aprendo com muita facilidade como também tem outras pessoas que aprendem com mais facilidades do que eu mais também existem pessoas que aprendem com um pouco de dificudade,como tem gente que aprende depois de muito tentar.Eu acho que isso não depende do profissional que ensina a matemática.Mais também depende da dedicação do aluno em se esforçar para aprender.Também se o aluno não quiser nada com a vida nunca essa pessoa vai se dar bem na matéria e enclusive muitas profissões hoje em dia requer o estudo da matemática por exemplo marqueting,engenharia e entre outras profissões.

  • 17. eder gomes&hellip  |  junho 21st, 2008 at 01:45:44

    é muito bom saber q tem sites desse tipo q esclarecem nossas dúvidas em relação a matematica! obrigado! pelas dicas!

  • 18. paloma&hellip  |  junho 26th, 2008 at 21:43:08

    adorei esse site aprendi e tirei todas minhas duvidas!!!
    love matemática

  • 19. Everaldo&hellip  |  agosto 2nd, 2008 at 18:47:21

    Muito bom, gostei muito do site, que contnue assim.

  • 20. katarina&hellip  |  agosto 14th, 2008 at 22:03:44

    por favor coloquem mais exemplos eu estou na 5 serie e preciso de estudar com exemplos bons e eu amei d+ esses!xau fikem com Deus

  • 21. Ivonilde Sabino&hellip  |  setembro 7th, 2008 at 21:22:00

    Muito bom esses exemplos de matemática do site.
    Parabéns….

  • 22. CAMILA&hellip  |  setembro 19th, 2008 at 16:07:54

    ESSE SITE É EDUCATIVO E CONTEM CONTEû DO BOM PARÀBENS.

  • 23. Roger&hellip  |  setembro 21st, 2008 at 22:15:45

    Otimo Site quem quiser me add no orkut ai só acessar o link por favor: http://www.orkut.com.br/Main#Profile.aspx?uid=11894321120630766940

    BLOG de ESTREMANTE UTILIDADE!

  • 24. Mirian&hellip  |  setembro 29th, 2008 at 15:45:28

    Maravilhoso!Meu filho conseguiu aprendewr fração através dete site, muito obrigada!

  • 25. Vinicius&hellip  |  outubro 2nd, 2008 at 09:19:04

    quero saber akelas fraçoes tipo 2 Quartos + 1 Quinto
    Tipo assim com o M.M.C = Minimo Multiplo Comun

  • 26. ISABELA&hellip  |  outubro 2nd, 2008 at 09:34:41

    MTO BOM.

  • 27. valeria&hellip  |  outubro 3rd, 2008 at 21:33:03

    me jude a faser esta fraçao 8,16 obrigado ……

  • 28. gabi&hellip  |  outubro 13th, 2008 at 16:45:31

    e legal e site.

  • 29. luiz eduardo&hellip  |  outubro 16th, 2008 at 21:03:20

    gostei obrigado me ajudou num trabalho da escola .amei esse site

  • 30. Jesica&hellip  |  outubro 17th, 2008 at 13:46:09

    me ajudem estou lok preciso saber esta fração 18+2×3 por 3 quartos me ajudem bjss

  • 31. leandra&hellip  |  outubro 23rd, 2008 at 08:35:31

    pow esse´site tem tudo que eu precisava e sempre turo as dúvidass aquiiiiii!!!!!!!!
    esse site é muito bommm , sempre que estiver com dúvidas venha akiiiii

  • 32. jullio&hellip  |  outubro 28th, 2008 at 20:19:02

    nossa gosto muito de matematica mas é algo que se tem que praticar se ñ esquece depois que sai da escola fiquei mais de 1 ano sem ver matematica quando vim estudar novamente esqueci coisas basicas como as operações das fraçoes é só um comentario pertinente rsrsr t+++

  • 33. erico&hellip  |  novembro 3rd, 2008 at 12:57:27

    mt bom…procurei mt na net mas nao achei isso…
    coisas básicas e faceis, mas que sao faceis de esquecer…
    detalhou bem e explicou bem…deu pra relemrbar tudo…

  • 34. karine&hellip  |  novembro 18th, 2008 at 17:29:40

    olha eu vou dizer a verdade eu odeioo matematica,nunk tirei nota boa em matematik,mas amanha eu tenho prova e esse site me ajudou muitooooooo quando eu receber minha nota eu publiko ela aqui ta vlww

  • 35. karine&hellip  |  novembro 18th, 2008 at 17:35:40

    ta eu entendiii tudooooo e bem facilll mas sera q a professora vai me dar nota boa aaaaaaa tomara eu sou d++++ linda lindaaaaaaa

  • 36. Marcela&hellip  |  novembro 26th, 2008 at 20:31:55

    Esse site é muito bom mais precisava de mais explicações

  • 37. Mah&hellip  |  novembro 26th, 2008 at 20:34:28

    Muitooo daora ess site Ameiii tirei tds as minhas duvidas

  • 38. luiza&hellip  |  fevereiro 5th, 2009 at 20:47:23

    nossa eu adoro matematica mas tem algumas coisas q nao consigo fazer mas com a ajuda desse site acho q sim vou conseguir…

  • 39. Marcelo&hellip  |  fevereiro 14th, 2009 at 23:35:56

    Preciso resolver um problema matamático onde se pede o seguinte:
    Gastei os 4/5 dos 5/8 do que possuia com pagamento do aluguel
    da casa em que moro, em seguida os 20% do resto com diversões. Com quantos % ainda fiquei?

  • 40. viiihH e reehH&hellip  |  março 4th, 2009 at 11:35:52

    eh mtoo legal esse saite tem tudu q vc precisa

  • 41. andressa&hellip  |  março 9th, 2009 at 00:14:09

    nooosa, muito bom o cyte, barabéns.

  • 42. veronica&hellip  |  março 31st, 2009 at 12:56:59

    noooooooohhhh mano a melhor professor e o pc mesmo viu……………….gamei

  • 43. lorena&hellip  |  abril 13th, 2009 at 20:24:32

    me ajude não entendi nada

  • 44. mariana&hellip  |  abril 14th, 2009 at 23:49:54

    nao consegui entender nada dessa porcariaaaaaaaa

  • 45. ivan silva pires&hellip  |  abril 25th, 2009 at 10:17:06

    eu entendi tudo bela revisão mas p vc entender matematica vc tem q ter uma basv se n vc n entende nada !!!

  • 46. Bruno&hellip  |  abril 26th, 2009 at 17:29:07

    Cara, naum entendi nada no meu livro. Ake tá super fácil de entender

    vlew

  • 47. jaqueline&hellip  |  maio 5th, 2009 at 13:00:11

    nao consigo entender nada

  • 48. Letícia Ingrid&hellip  |  maio 12th, 2009 at 17:30:58

    falta exercícios, fala sério! Na prova não vai cair só teoria!

  • 49. ana clara&hellip  |  maio 13th, 2009 at 15:15:38

    eu achei o maximo !!!!!!!!
    sem comentario bjs !!!!!!!!!!!!!!!

  • 50. kqmilq&hellip  |  junho 3rd, 2009 at 18:42:01

    eu achei bem legal nos aprendemos e nos divertimos deixando nosso comentario bjs abracos

  • 51. vitor&hellip  |  junho 15th, 2009 at 17:25:57

    Queria saber como se faz para obter frações inversas….
    Eleva a -1?

  • 52. natasha&hellip  |  julho 23rd, 2009 at 18:04:32

    do seu salario de332,40vc gasta 2/8com mroradia3/8com alimentação sobrando para as demais despeza

  • 53. wellington tatsunori asah&hellip  |  julho 24th, 2009 at 20:53:26

    esse site é bom , + c vc vai fasera faculdade entre no site http://www.scribd.com , eu achei esse site pelo bing (msm coisa que google , + é um novo)+ acho q vai dar certo vc entra pelo site direto

  • 54. Vitória&hellip  |  agosto 12th, 2009 at 12:51:51

    Eu qeero so operaçoes

  • 55. jullyana&hellip  |  agosto 20th, 2009 at 12:24:05

    euu naoo entendii nadaa dessee troosoo hojee tenhoo provaa e numm seii nadaa aff

  • 56. mateus&hellip&hellip  |  setembro 2nd, 2009 at 16:50:05

    gostei muito desse troso to na 5 serie ea minha professora e um grudeeeeeeeeeeeeeeeeeee!!!!!!!!!!!!

  • 57. Thiago&hellip  |  setembro 7th, 2009 at 21:20:49

    Eu não achei bem o que eu procurava

  • 58. cinthia&hellip  |  setembro 14th, 2009 at 10:04:56

    eu nao achei o que eu bem procurava
    mas eu apredi muito
    beijooooooooooooooossssssssss!!!!!!!!!!
    fuiiiiiiiiiiiiiiii!!!!!!!!!!!!!!!!!!!!!!!!!!

  • 59. elisa&hellip  |  setembro 23rd, 2009 at 11:53:11

    eu não achei o que eu procurava

  • 60. sanara&hellip  |  outubro 6th, 2009 at 23:00:09

    Gostei !!! Muito obrigada .. BjOss ..

  • 61. Iara&hellip  |  novembro 10th, 2009 at 17:34:34

    ótimo o site, achei tudo que queria e muito bem explicado
    parabens!

  • 62. Dario Santos dos Anjos&hellip  |  novembro 15th, 2009 at 04:58:21

    Obrigado, é muito bom ter na rede páginas como esta. Encontrei exemplos ótimos parabens!

  • 63. Bruno&hellip  |  dezembro 1st, 2009 at 22:06:51

    E como faço para diminuir uma fração de um numero inteiro.

    Por Exemplo: 6/4 – 9

    (6/4 é 6 sobre 4) menos numero inteiro 9

  • 64. arthur&hellip  |  dezembro 7th, 2009 at 12:23:08

    gostei do conteúdo

  • 65. gleiçe&hellip  |  dezembro 8th, 2009 at 19:10:08

    Ameiii a explicaçãoo

  • 66. Juliana Rodrigues de Jesu&hellip  |  dezembro 9th, 2009 at 13:45:40

    eu adorei as explicações que deram espero procurar mais coisas e que vocês possam dar as explicações sejam vocês.

    beijos de : Juliana

  • 67. leticia&hellip  |  dezembro 13th, 2009 at 18:27:12

    EU ACHEI ESSE SITE MUITO OTIMO MAS TINLHA QUE TER MAS OPERAÇOES COMO POTENCIAÇAO, RADICIAÇAO ,SO MAS SE VC COLOCAR VC VAI VER VAI SER MUITO MAS ASESSADO ……………..

  • 68. anna&hellip  |  dezembro 20th, 2009 at 20:21:02

    eu queria sabe o que é fração:operação,potenciação,expressões

  • 69. giovanna fabri rodrigues&hellip  |  março 15th, 2010 at 12:58:32

    nao gostei de nada,quem fez isto fez mt maul feito!!

  • 70. Gisele&hellip  |  março 28th, 2010 at 19:00:14

    Eu estou procurando exercícios com frações( adição, subtração, multiplicação e divisão).
    Por favor, adiciona?
    Obrigada.
    Gisele

  • 71. Lindalva Martins dos Sant&hellip  |  março 29th, 2010 at 15:14:56

    Obrigada, gostei das explicações, só que eu queria mesmo era um outro método para resolver frações com denominadores diferentes.

    Obrigada, um abraço.

    Lindalva.

  • 72. Lindalva Martins dos Sant&hellip  |  março 29th, 2010 at 15:25:07

    Obrigada, gostei dos assuntos só que eu queria era um outro método para calcular adição e subtração de frações com denominadores diferente.

    Nada mais o momento um abraço.

    Lindalva Martins.

  • 73. lucas&hellip  |  abril 3rd, 2010 at 17:52:12

    muito massa esse site falo!!!!!!!!!!!!!!!!

  • 74. ernesto&hellip  |  maio 29th, 2010 at 10:43:02

    Muito bem explicado!!

  • 75. jessica silva&hellip  |  junho 7th, 2010 at 22:48:43

    eu adorei este site, eu tinha dúvidas, mas, acabei com elas

Deixe seu Comentário

Obrigatório

Obrigatório, (não publicado)

São permitidas as seguintes tags:
<a href="" title=""> <abbr title=""> <acronym title=""> <b> <blockquote cite=""> <cite> <code> <del datetime=""> <em> <i> <q cite=""> <strike> <strong>

Trackback this post  |  Subscribe to the comments via RSS Feed

Notifica, via E-Mail, sobre novos artigos publicados no VICHE. Ao fazer sua inscrição você receberá uma mensagem em inglês no E-Mail informado abaixo, com um link, para que o serviço seja ativado. Basta então clicar nesse link para que você passe a receber as notificações.

Delivered by FeedBurner