Definições

Proporção é a sentença matemática que exprime a igualdade entre duas razões (veja definição e propriedades na parte I) e é representada por:

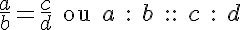
onde b e d são diferentes de zero.

Na expressão acima, b e c são chamados de meios e a e d de extremos; a e c chamam-se, também, de antecedentes da proporção e b e d de consequentes.

Formas comuns de leitura de uma proporção: a esta para b assim como (::) c está para d ou simplesmente, a sobre b iguala (é igual a) c sobre d.

Quarta proporcional de três números dados é um quarto número que forma uma proporção com os números dados.

Proporção contínua é uma proporção que tem os meios iguais. Exemplos:

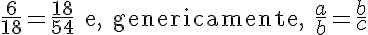
Terceira proporcional de dois números a e b é um terceiro número c que esteja em proporção contínua com os dois primeiros, de modo que se tenha:

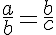
Propriedades

P1. Em toda proporção, o produto dos extremos é igual ao produto dos meios. Ou seja, dada a proporção:

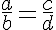teremos que .

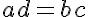Certamente a grande maioria dos alunos que já tiveram oportunidade de conhecer o assunto, sabe de “cor e salteado” essa propriedade e que os cálculos devem ser efetuados com o uso do famoso “x”, ligando os meios e os extremos da proporção. Mais porque isso é verdadeiro, talvez, muito poucos. A seguir vamos mostrar o porque da propriedade.

Antes, abrimos um parêntesis para recapitular as propriedades de uma igualdade, que você deve ter visto nos primórdios de seu aprendizado matemático e que são utilizadas em várias situações, como por exemplo, na solução de equações do primeiro grau – os famosos passa para o outro lado e troca de sinal ou o termo constante antes da incógnita x vai para o outro lado dividindo. Eis as tais propriedades:

1. Se a = b então a + c = b + c (ou seja, somando-se o mesmo valor c aos dois lados da igualdade esta não se altera);
2. Se a = b então a – c = b – c (explicação semelhante);
3. Se a = b então a/c = b/c, c diferente de zero (ou seja, dividindo-se os dois lados de uma igualdade pelo mesmo número ela não se altera);
4. Se a = b então a.c = b.c (ou seja, multiplicando-se os dois lados de uma igualdade pelo mesmo número ela não se altera).

Demonstração da propriedade P1: Com efeito, multiplicando-se as duas razões (na igualdade) pelo produto dos consequentes b e d a igualdade não se altera (pela propriedade 4 de uma igualdade) e obtemos que:

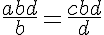
e simplificando (dividindo) no primeiro membro b no numerador e b no denominador e no segundo d, da mesma forma, obtemos que ad = cb.

P2. Reciprocamente, se quatro números são tais que o produto de dois deles seja igual ao produto dos outros dois, esses quatro números formam uma proporção. Ou seja, dados a, b, c e d, com b e d diferentes de zero, e se ad = bc [1] então:

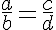
Demonstração: Simples, basta utilizar a propriedade 3 de uma igualdade dividindo ambos os termos da igualdade [1] por bd. Faça as contas e você verá que se obtém o resultado esperado.

Como consequência das propriedades P1 e P2 podemos dizer que a condição necessária e sufiente para que quatro números estejam em proporção é que o produto dos extermos seja igual ao dos meios. Além do mais, temos que:

1. Ao alternarmos os meios de uma proporção, ainda teremos uma proporção, uma vez que as propriedades P1 e P2 permanecem válidas;
2. Ao alternarmos os extremos de uma proporção o mesmo se aplica;
3. Ao invertemos as duas razões.

P3. Quando duas proporções têm uma razão em comum, as duas outras razões dessas proporções também se acham em proporção. Ou seja, se:

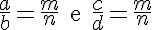
então:

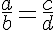
P4. Em toda proporção, a soma ou a diferença dos dois primeiros termos está para o primeiro ou para o segundo como a soma ou a diferença dos dois últimos está para o terceiro ou o quarto. Isto é, dada a proporção:

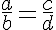
então:

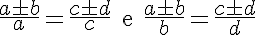
P5. Em toda proporção, a soma ou a diferença dos dois primeiros termos está para a soma ou a diferença dos dois últimos como o primeiro termo esta para o terceiro ou como o segundo está para o quarto. Isto é, dada a proporção:

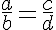
então:

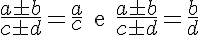
P6. Em toda proporção, a soma dos dois primeiros termos está para a sua diferença assim como a soma dos dois últimos está para a sua diferença. Isto é, dada a proporção:

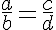
então:

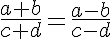
P7. Em toda proporção, a soma dos dois primeiros termos está para a sua diferença como a soma dos dois últimos está para a sua diferença. Ou seja, dada a proporção:

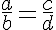
então:

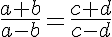
P8. Quando se multiplicam, membro a membro, várias proporções, os produtos forma uma proporção. Em outras palavras, sejam as proporções:

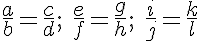
então:

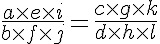
P9. Quando quatro números se acham em proporção, suas potências do mesmo grau também se acham em proporção. Em outras palavras, sejam a proporção abaixo e m um inteiro positivo maior do que 1:

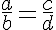
então:

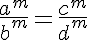
Observe que as propriedades P8 e P9 podem ser adaptadas para a divisão e raízes de mesmo índice respectivamente. Fica como exercício o estabelecimento dessas novas propriedades.

Referência:

Elementos de Aritmética, Curso Superior – Para o curso colegial e admissão às escolas superiores, do Irmão Isidoro Dumont, Coleção de Livros Didáticos F. T. D, publicado em 26/10/1945