Adição
É a operação que tem por fim determinar uma fração que contenha todas as unidades e partes de unidades de várias parcelas de mesma natureza.
Entende-se por mesma natureza as frações que exprimem as mesmas partes da unidade, ou seja, que tenham o mesmo denominador, também conhecidas como homogêneas (2/8, 3/8 e 5/8 é um exemplo de tais frações).
Distinguem-se três casos na adição de frações.
A1. Soma ou adição de frações homogêneas ou de mesmo denominador.
Como fazer – Somam-se os numeradores e conserva-se o denominador comum.
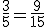 . Veja que a segunda fração é obtida a partir da primeira multiplicando-se o seu numerador e seu denominador por 3. Inversamente, a primeira é obtida da segunda dividindo-se o seu numerador e seu denominador, também, por 3.
. Veja que a segunda fração é obtida a partir da primeira multiplicando-se o seu numerador e seu denominador por 3. Inversamente, a primeira é obtida da segunda dividindo-se o seu numerador e seu denominador, também, por 3.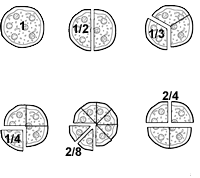 Para que a apresentação do assunto em um único artigo não fique demasiadamente extenso, ele será dividido em duas ou mais partes. A primeira aborda um pouco de história das frações, cujo texto foi extraído da
Para que a apresentação do assunto em um único artigo não fique demasiadamente extenso, ele será dividido em duas ou mais partes. A primeira aborda um pouco de história das frações, cujo texto foi extraído da 




Comentários Recentes