Esta matéria aborda o conceito e propriedades de sequência ou sucessão, com ênfase nas que possui uma fórmula bem definida que permite calcular qualquer um de seus termos. Ou seja, das sequências que possuem uma lei de formação que estabelece uma relação entre o valor de seus termos e sua posição.
Especificamente, das duas mais conhecidas: a Progressão Aritmética (PA) e a Progressão Geométrica (PG), dividido em três partes (a primeira este artigo e as demais serão publicadas oportunamente):
- Parte I – teoria sobre PA;
- Parte II – teoria sobre PG;
- Parte III – exercícios resolvidos sobre PA e PG.
Mas antes precisamos conhecer a definição do que seja uma sequência ou sucessão.
Sequências ou Sucessões
Uma sequência ou sucessão é um conjunto ordenado (finito ou infinito) de elementos de qualquer natureza, em que cada elemento fica naturalmente seqüenciado.
Um conjunto ordenado é um conjunto que possui uma relação de ordem.
E uma relação de ordem é definida para pares de elementos de um conjunto S, e têm que, necessariamente, possuir três características:
- anti-simetria: para todo
 e
e 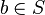 ,
,  ou
ou 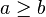 ;
;
- se
 e
e 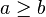 , então
, então  ;
;
- transitividade: se
 e
e  , então
, então 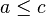 .
.
São exemplos de sequências:
- sequência dos dias da semana: domingo; segunda-feira; terça-feira; quarta-feira; quinta-feira; sexta-feira; sábado;
- sequência dos 100 primeiros números inteiros positivos: 1; 2; 3; … ; 98; 99; 100;
- Os números de Fibonacci (esta seqüência foi descrita primeiramente por Leonardo de Pisa, também conhecido como Fibonacci (c. 1200), para descrever o crescimento de uma população de coelhos): 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946…
Note que todos os exemplos possuem as três características definidas na relação de ordem.
A título de ilustração, abrindo um parênteses, apresento a seguir a fórmula recursiva que define os números de Fibonacci (n pertencente ao conjunto dos números Naturais):

Na prática: você começa com 0 e 1, e então produz o próximo número de Fibonacci somando os dois anteriores.
A representação de uma sequência é feita escrevendo-se seus elementos, ou termos, entre parênteses. Assim, o segundo exemplo acima, é representado por:
(1; 2; 3; … ; 98; 99; 100)
Da definição de sequência, onde a ordem de seus elementos é uma condição necessária, temos que:
( 1; 3; 5; 7; 9; 11) é diferente de (1; 3; 7; 5; 9; 11)
Genericamente, sua representação pode ser escrita como:
(a1; a2; a3; …; an-1; an; …)
onde n pertence ao conjunto dos números naturais positivos. Os índices indicam a posição dos termos na sequência (a1 representa o primeiro termo, an representa o enésimo termo, …).
Formalmente, uma sequência ou sucessão numérica pode ser definida como uma função dos números naturais menos o zero em R:
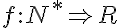
Uma sequência numérica é finita se o domínio de f é finito, isto é, i varia de 1 a n pertencente ao conjunto dos números Naturais (i = 1, 2, …, n), também conhecida como n-upla. E infinita quando o domínio é o próprio conjunto dos números Naturais positivos (i = 1, 2, …., n-1, n, …).
Três termos consecutivos qualquer de uma sequência podem ser representados por:
an-1, an, an+1
onde an-1 é o antecessor de an e an+1 é o sucessor de an.
Lei de Formação
Interessam à Matemática as sequências numéricas para as quais é possível estabelecer uma lei de formação, ou seja uma fórmula que permita calcular qualquer um de seus termos. Ou em outras palavras as sequências numéricas em que seus termos se sucedem obedecendo a uma regra.
Estas leis de formação podem ser apresentadas das maneiras a seguir:
a) Por Recorrência
São dadas duas ou mais regras: uma (ou mais) que define os termos iniciais da sequência e outra para calcular os demais termos a partir de antecessores.
Exemplos:
- Os números de Fibonacci: definidos a1 = 0 e a2 = 1 e a regra F(n-1) + F(n-2) que corresponde à soma dos dois antecessores para definir os demais termos;
- a1 = 5, an = an-1 + 3 e n = 5: a1 = 5, a2 = a1 + 3 = 8, a3 = a2 + 3 = 11, a4 = a3 + 3 = 14, a5 = a4 + 3 = 17 => (5; 8; 11; 14; 17)
b) Em função do índice da sequência (posição)
Exemplos:
- an = 2n + 3, n = 1, 2, 3, 4, 5: (5; 7; 9; 11; 13);
- an = 2n, n Natural diferente de zero: (2; 4; 8; 16; …).
c) Por propriedade dos termos
Exemplos:
- A sequência cujos termos são os primeiros cinco números primos: (2; 3; 5; 7; 11);
- A sequência dos números inteiros ímpares menores do que 20: (1; 3; 5; 7; 9; 11; 13; 15; 17; 19).
Progressões Aritméticas (PA)
Define-se progressão aritmética como toda sequência numérica em que cada termo, a partir do segundo, é igual à soma de seu antecessor por um número constante r. r é denominado a razão da PA. Em símbolos:
an = an-1 + r (n >= 2)
As PA são classificadas em três tipos:
Uma PA é crescente quando r > 0, ou seja, quando cada termo é maior do que seu antecessor (claro, a partir do segundo). De fato, da definição decorre que:
an – an-1 = r > 0 <==> an – an-1 > 0 <==> an > an-1
Uma PA é constante quando r = 0, ou seja, quando cada termo é igual ao antecessor:
an – an-1 = r = 0 <==> an – an-1 = 0 <==> an = an-1
Uma PA é decrescente quando r < 0, ou seja, quando cada termo é menor do que seu antecessor:
an – an-1 = r < 0 <==> an – an-1 < 0 <==> an < an-1
Fórmula do Termo Geral de uma PA
Seja (a1; a2; a3; …; an-1; an; …) uma PA qualquer de razão r. Então seu enésimo termo (an) é:
an = a1 + (n – 1)r
Demonstração:
Sabemos, da definição de uma PA, que a diferença entre cada termo e seu antecessor é igual a razão, isto é:
a2 – a1 = r, a3 – a2 = r, a4 – a3 = r, …, an – an-1 = r
Somando, membro a membro, estas n – 1 igualdades, obtemos:
a2 – a1 + a3 – a2 + a4 – a3 + … + an – an-1 = (n – 1)r
Cancelando os termos comuns:
-a1 + an = (n – 1)r => an = a1 + (n – 1)r
Observações:
- Da definição decorre que uma PA fica determinada quando conhecemos o primeiro termo e a razão;
- Em uma PA finita a1 e an são denominados os seus extremos e os demais termos os meios aritméticos;
- A fórmula do termo geral de uma PA nos diz que para calcular o termo de ordem n é suficiente somarmos (n – 1) vezes a razão ao primeiro termo;
- Do mesmo modo, essa fórmula permite calcular o número de termos de uma PA finita conhecendo-se seus extremos e a razão.
Termos Equidistantes dos Extremos
Dados os dois termos ap e aq de uma PA finita com n termos, dizemos que eles são equidistantes dos extremos se o número de termos que antecedem ap – (p – 1) termos – é igual ao número de termos que sucedem aq – (n – q) termos.
Da definição vem que:
p – 1 = n – q => p + q = n + 1
Essa relação nos permite dizer, por exemplo, que em uma PA finita com 30 termos, o termo 6 é equidistante do 25, uma vez que 6 + 25 = 30 + 1.
Soma dos termos de uma PA finita
Antes de deduzir a fórmula da soma dos n primeiros termos de uma PA finita, vamos demonstrar a seguinte propriedade:
PA1. Em uma PA finita, a soma de dois termos equidistantes dos extremos é igual à soma dos extremos.
Demonstração:
Sejam ap e aq dois termos equidistantes dos extremos de uma PA finita com n termos. O que vamos provar é:
ap + aq = a1 + an
Pela fórmula do termo geral:
ap = a1 + (p – 1)r e aq = a1 + (q – 1)r
Somando os membros das igualdades obtemos:
ap + aq = a1 + (p – 1)r + a1 + (q – 1)r = a1 + a1 + (p + q – 2)r
Substituindo p + q (veja definição acima):
ap + aq = a1 + a1 + (n + 1 – 2)r = a1 + a1 + (n – 1)r
E pela definição do termo geral de uma PA:
ap + aq = a1 + an
PA2. A soma dos n primeiros termos de uma PA é dada pela fórmula:

Demonstração:
Pela propriedade PA1 temos que (note que a soma de todos os índices de cada parcela é igual a n + 1, e portanto, equidistantes dos extremos):
a2 + an-1 = a3 + an-2 = … = a1 + an
Por outro lado:
Sn = a1 + a2 + … + an
=> Sn + Sn = 2Sn = (a1 + an) + (a2 + an-1) + … + (an + a1)
onde ordenamos as parcelas convenientemente, primeiro termo do primeiro Sn com o último do segundo, e assim por diante, de modo a obter n parcelas iguais a a1 + an. Logo:
2Sn = (a1 + an)n => Sn = [(a1 + an)n]/2 c.q.d.
PA3. A soma dos n primeiros inteiros positivos é:

Demonstração:
Consequência direta de PA2, uma vez que a1 = 1 e an = n.
Referências:
- Fundamentos de Matemática Elementar, Gelson Iezzi, Osvaldo Dolce & Carlos Murakami, São Paulo, Atual Editora Ltda, edição 1977;
- Matemática para o Ensino Médio: Volume Único, Manoel Jairo Bezerra, São Paulo, Editora Scipione, 2001;
- Wikipédia – Sequência Matemática.


fev 23, 2011 @ 09:44:50
não entendi muuito bem =x
dez 25, 2009 @ 14:52:25
kara e meio louco essa materia , mas obrigado por vcs existirem , pois só assim podemos tirar nossa duvidas.. vsleu…
ago 11, 2009 @ 08:48:02
é sempre agradável e satisfatório quando se tem páginas como estas que serve milhões da pessoas no mundo. existam par sempre obribado
jul 06, 2009 @ 23:36:31
otimo site porem quase não tem exemplos com numeros e confunde quem esta iniciando, por favor de exemplos de uma PA constante e equidistante
maio 26, 2009 @ 21:28:59
EU E MINHA GALERA ODIAMOS ESSA MATERIA!!!!!!!!
maio 24, 2009 @ 22:14:00
determine o numero de termos da P.A. 5,8…62.
maio 17, 2009 @ 12:33:32
qual é a sequencia do termo geral a=2n-1
maio 15, 2009 @ 17:27:32
AAAAAAAAAAAAAAAFE QUE TROÇO , NAO ENTENDI NADA !
fev 19, 2009 @ 16:44:43
gostei muito da maneira que vocês explicaram o assunto foi de uma maneira muito ampla, mas com tudo ainda fiquei sem entender um pouco
out 07, 2008 @ 10:42:23
gostaria de saber o calculo do vigésimo termo da pa (1,6,11)
jun 11, 2008 @ 09:40:58
poxa adorei foi otimo pois e ajudou muitOO obrigadinha…
abr 04, 2008 @ 10:01:12
este sitio de vocês é muito bom gostaria que vocês me enviassem sempre alguns e-mails sobre matemática, física, química e biologia do ensino médio, valeu!!!
abr 02, 2008 @ 22:10:28
Tem como mandar no meu e-mail a sequencia de uma PA?
O que é sequencia na ” Progressao Aritmetica?
Amei o site…
mar 24, 2008 @ 15:52:02
Parabéns pelo site, as explicações são ótimas e tirou muitas dúvidas relacionadas. Sou formado em Matemática. UM ABRAÇO!!!
mar 19, 2008 @ 14:22:52
estou em dúvidas quando é dado os termos de umaP.A. (2,4 , 6 ,……) sabendo que a1=2 e a9 =18 descreva essa p.A. Essa P.A. é finita ou infinita como descrevê-la. outro exemplo dao a P.A.( 10,60, 70…. ) qual a localização do número 100. Descreva essa P.A.
mar 16, 2008 @ 02:36:28
achei técnico d+ faltou um pouco mais de exemplos com numeros
jan 16, 2008 @ 10:02:56
Agradeço a equipe que montou este material, estava precisando dar uma relembrada na matéria e o material está sendo de grand valia….Obrigado e continuem assim….
dez 16, 2007 @ 20:03:26
Preciso resolver o seguinte problema
a3+a6=34 e a4+a9=50. Calcule a soma dos 20 primeiros termos dessa PA.
dez 10, 2007 @ 11:52:19
a explicação está muito boa, mas acho q poderia citar exemplos com numeros, para alguns é muito mais fácil de entender…parabéns, obrigada!
nov 06, 2007 @ 17:39:20
valeu pelos tokes em PA e PG é bom ter ainda pessoas legais com assuntos maneiros
out 03, 2007 @ 12:10:46
Sou professor de matematica de 8ª série com puoca experiencia em preparação para provas como a do SAEB, por esse motivo gostaria de receber questões matematicas referente a essa prova que será realizada mes de movembro.
obrigado!
jul 24, 2007 @ 18:24:10
Obrigado por tudo ótimo site, espero vcs botem mais explicações e exercícos.
Valeu
jun 24, 2007 @ 14:00:33
Como se originou as progressoes?
Qual foi o matematicoi que realizou os primeiros trabalhos? Em que ano?
jun 12, 2007 @ 17:11:26
!!!OI!!!
FAÇO CURSO DE LICENCIATURA EM MATEMÁTICA: E GOSTARIA QUE SEUS ARTIGOS ESPLANACEM BASTANTE AS NOVAS TENDÊNCIAS DA EDUCAÇÃO MATEMÁTICA!!!
ATENCIOSAMENTE!!!
abr 05, 2007 @ 10:22:50
olá,
Sou mestre em matemática pura( análise não linear). Achei q seria interessante acrescentar um pouco mais sobre o conceito de sequência.
mar 15, 2007 @ 16:38:08
Não é um comentario. sim uma dúvida neste exemplo que temos a1=4 e r=-3(4,1,-2,-5) não entendi a resposta poderiam me ajuda nesta dúvida, agraeço desde já.
fev 27, 2007 @ 19:44:19
Oii
Ótimo o site, mais não consegui esclarecer minha duvida…vocês poderiaum me responder se uma seuquencia pode ser PA e PG ao mesmo tempo, se a rsponsta for positiva por favor me mande um exemplo.
Obrigada!
dez 11, 2006 @ 21:29:13
quero que me ajudem
a soma dos numeros inteiros e positivos menores que 100, que soa divisiveis por 7 é:
me ajudem por favor….
dez 11, 2006 @ 15:29:18
Se possível mande explicações de P.G para o meu e-mail
nov 24, 2006 @ 14:03:35
nao esta o q eu qeria mas obrigado.. devia ter mais coias sobre a matematica
Viche » Curiosidade Matemática #5 - Método de Pitágoras para Calcular a Potência de Grau 2 de um Número
nov 19, 2006 @ 21:57:10
[…] é uma Progressão Aritmética (PA) de razão r = 2, onde an representa o enésimo termo ou o enésimo número ímpar. […]
out 16, 2006 @ 11:30:49
Ei adorei tudo bem explicado espero que eu consiga tirar a nota que eu mereço.
beijos,beijos,beijos,beijos,beijos.
set 14, 2006 @ 16:46:23
Vocês são ótimos,mandem E-mails para mim contendo explicações sobre P.A.
set 04, 2006 @ 19:39:39
Amei!
Tudo muito bem explicado…
É uma aula mermu…
Espero q contunue assim…
VALEU!
ago 28, 2006 @ 17:19:52
gostei muito da explicação irá me ajudar realmente no desenvolvimento do meu trabalho.
ago 15, 2006 @ 22:21:18
Muito bom a página de vocês, parabéns, voltei a estudar e já tirei algumas dúvidas aqui, faço matemática.